(This is the concluding part of the sequel to ‘Introduction to Ganita’)

Part 1 (Introduction) 

Part 2 (Ganita – Math Encounters)

Part 3 (below): Ganita prevailed over Math in their encounters, but what did it really win? While Ganita’s results were absorbed into Mathematics, the underlying pramana and upapattis were rejected. We explain why this happened, and its implications.

Digestion Of Ganita, the Needham Question, and the Road Ahead

Nothing in life is to be feared, it is only to be understood. Now is the time to understand more, so that we may fear less - Marie Curie.

The Digestion of Ganita

It appears the ancient Babylonians had something in common with the Indians: they were pattern-seekers. As far as trying to understand how the world around us works, Richard Feynman rejected (Greek) Mathematics in favor of what he recognized as a Babylonian method, as discussed in this lecture below. Despite this endorsement, it is the Greek approach that drives Mathematics today, while the Babylonian culture can be found only in famous museums today. Why?

It would not be a problem for any civilization to view and benefit from imported knowledge by employing a native lens, without denigrating and destroying the external source tradition, and based on mutual respect. However, when knowledge from another culture is deliberately cannibalized and appropriated as a predator, it is a serious problem. It turns into a process known as’digestion‘. We now describe how Ganita was digested into Mathematics after their encounters.

The Digestion of Ganita into Mathematics

This process of digestion has been laid out by Rajiv Malhotra in [4]. We apply this description step-by-step to see how Ganita was digested into Mathematics.

Step 1. “The less powerful culture is assimilated into the dominant one in such a way that: the dominant civilization dismembers the weaker one into parts from which it picks and chooses which pieces it wants to appropriate“.  During their encounter, all the important results of Ganita, starting from the place value system with zero, to algebra, trigonometry, algorithms, combinatorics, … to calculus were accepted by Europe to obtain real-life benefits. However, the underlying epistemology and approach of Ganita that has worked so well for 2000+ years, and could be used to generate such astonishing results in the future were amputated from Ganita. Only the results were retained within Mathematics.

Step 2. “appropriated elements get mapped onto the language and social structures of the dominant civilization’s own history and paradigms, leaving little if any trace of the links to the source tradition“. The formal Math rooted in the Greek tradition was enhanced and expanded so that the Ganita results could be systematically re-derived and reinterpreted in a compatible manner. Later, the beneficial features of the native Encuvati system of pedagogy was appropriated into the British teaching approach, and ‘undesirable’ features were deleted to ensure compatibility with ‘Christian values’ [15]. Once this process was complete, the source tradition of Ganita was expendable.

Step 3. “the civilization that was thus mined gets depleted of its cultural and social capital because the appropriated elements are modified to fit the dominant civilization’s own history, and these elements are shown to be disconnected from, and even in conflict with, the source civilization“.

A. The credit for a re-engineered calculus was given to Newton/Leibniz and not Madhava and the Kerala School. We are taught the Pythagoras theorem and proof, not Baudhayana’s result and validation procedure. Fibonacci numbers, not Gopala-Hemachandra series. The IEEE journals recognize Arab numerals, not Hindu numbers, and so on. The list is long. In almost all these cases, the standard reason is that the Indians had not proved their results using the formal system devised by the west, even though each of these results were generated first by Ganita and also satisfactorily validated within the source tradition, often centuries earlier. The Ganita tradition was erased from the history of Mathematics.

B. On the other hand, the following types of claims are created:

• Vedanga Jyotisha was full of astrology and religious mumbo-jumbo
• Ganita was some kind of elite “Vedic Mathematics”
• Hindu tradition was backward, caste-ridden, superstitious and incapable of producing such advanced scientific results.

Whereas, the exact opposite is true.

• Vedanga Jyotisha is the science of time-keeping, and “the entire Jyotisa does not have a single sentence relating to astrology or prophecy” [1], whereas the main goal of European calendar reform was to advance the cause of organized religion [1]
• Ganita was pragmatic and accessible to ordinary Indians including vegetable vendors who taught the greatest Arab scholar of their time [14], while today’s formal Mathematics is indeed the preserve of an elite few [1].
• Hinduphobia is rampant in the Humanities departments of Western universities, which is subsequently exported to Indian universities, even as the digestion of Hindu science and technology results continues unabated [16].

Step 4. The final result is catastrophic for the source civilization: “the depleted civilization enters the proverbial museum as yet another dead culture, ceasing to pose a threat to the dominant one. After being digested, what is left of a civilization is waste material to be removed and destroyed.”  A mathematical monoculture was imposed on India during the colonial era after uprooting the ‘beautiful tree‘, India’s indigenous decentralized education system whose Ganita curriculum was sensitive to local requirements. Few students and teachers in Indian schools and universities today are aware of the source Ganita tradition. Among those who recognize the word,  few realize it is not an Indian neologism for Mathematics. Is this not an instance of cultural genocide?

How can we protect and revive the authentic and practical Ganita tradition that was the head of all the Indian sciences? To do this, we must identify the nature of the civilizational ‘Poison Pills’ within Ganita.

Civilizational Poison Pills

Rajiv Malhotra introduced the idea of civilizational poison pills from an Indian perspective in ‘Indra’s Net’. [13]. “Poison pills are those elements or tenets that cannot be digested into the DNA of a predator, because consuming them would lead to the destruction of the predator’s constitution. If a predator absorbs such an element, it will mutate so profoundly that it will lose its original identity and qualities.”  We now try to identify the poison pill in Ganita that needs to be preserved.

Ganita’s Poison Pill

The Indians achieved a smart reduction in uncertainty in calculations to a contextually admissible level, instead of beating themselves up trying to attain complete certainty. Ganita and Vedic thought recognizes that human understanding of the cosmos is never fully complete. In [4], the Indian and western mindset is compared thus: “Indians indeed find it natural to engage in non-linear thinking, juxtaposing opposites and tackling complexities that cannot be reduced to simple concepts or terms. They may be said even to thrive on ambiguity, doubt, uncertainty, multitasking, and in the absence of centralized authority and normative codes. Westerners, by contrast, tend by and large to be fearful of unpredictable or decentralized situations. They regard these situations as problems to be fixed. As we shall see, there is in fact some scholarly evidence that demonstrates this view of Western attitudes.” For a mindset that revels in perfection, this element of uncertainty that was acceptable within Ganita is a poison pill. This anxiety was evident in all stakeholders in Europe during the Ganita-Math encounters.

Western Fear of Uncertainty

Practically every Western point of view from the ultra-secular, to the religious during the Ganita-Math encounters was in conflict with Ganita’s poison pill:

• In the abacus-algorismus battle, Ganita’s idea of ‘one manifesting as many’ in its place value system and the way it managed non-representability was suspect, given the scope for ‘chaos’ and ‘fraud’.
• For a reasoning mind like Descartes, measuring the ratio of curved to straight lines involved an irreducible uncertainty, an understanding of which was beyond the human mind. This gave rise to the term ‘irrational numbers’ [1]. Not surprisingly, he rejected the idea of infinitesimals too.
• Philosopher Thomas Hobbes was no friend of the Jesuits. But he too found the absolute, perfect order found in Euclidean geometry was its most appealing aspect and reflected his own perspective. As noted in [12] “in their deep structure, the Jesuit papal kingdom and the Hobbesian commonwealth are strikingly similar. Both are hierarchical, absolutist states where the will of the ruler, whether Pope or Leviathan, is the law.”
• The Jesuits, Protestants, Eastern Orthodoxy, Anglicans, and a vast majority of Christian sects may have disagreed on some theological points, but all subscribed to the history-centric truth claims of the Nicene Creed [4]. At least three aspects of Mathematics would’ve appealed to them:
  • Calendar and time-keeping helped preserve history centric dogma and reestablish the importance of clergy.
  • The top-down, hierarchical perfect Eucliean order.
  • Proving theorems without need for empirical demonstration. History-centric Christianity treats the body as a vessel of original sin. Embodied knowing is problematic for this mindset.
• Pioneer Jesuat monk Cavalieri underwent an inner struggle [12] after ingesting this poison pill, and all but disowned his Ganita-based idea of ‘indivisibles’.
• Scientists who championed the cause of the infinitesimals, and their successors could never come to grips either. The Tagore-Einstein conversation is a good example. As mentioned in [4] “Not even Einstein was able to reconcile himself to the uncertainty inherent in quantum mechanics, prompting him to remark: ‘God does not play dice with the universe.’ But Shiva and Parvati, the Hindu cosmic couple, do happily play dice. Indian philosophy is receptive to the uncertainty theories of physics.“

See Article 

However this poison pill does not negatively impact the Indian mindset. Why? Our Ganita Post discusses in detail, but we briefly summarize here for the sake of completion.

Ganita’s Comfort in Dealing with Uncertainty

The Indians were comfortable working with contextually accurate estimates for non-quantities like √2 and π, recognizing that the result could be improved upon.  Hindu society has no central authority that could ban innovation or the exploration of the realms of uncertainty. Its decentralized structure produced independent thinkers and innovators in every era. Dharma systems have built-in safeguards against Hobbesian/Church absolutism. As Rajiv Malhotra explains in [4] “Chaos is entrenched in the Vedas, the Puranas and Hinduism in general for a reason: its role is to counterbalance and dilute any absolutist tendencies as well as provide creative dynamism through ambiguity and uncertainty.” Ganita inherits all these features, and must retain all these properties for best results.

The inevitability of uncertainty was no cause for panic. It even opened up a degree of freedom for (dharmic, ethical) optimization using Yukti.  This comfort with uncertainty is visible right through Ganita’s storied history from Paanini‘s Ashtadhyayi before the common era, to the Aryabhatiya in the 5th century C.E, within the calculus results of Madhava in the 14th century, to Ramanujan in the 20th century. This perspective placed the Indian creation of all its algorithms, interpolations, calculus, etc. on solid epistemological ground. Let’s look at the Aryabhatiya, as an example.

Aryabhata‘s R-sine difference table shown below required an algorithmic package that managed uncertainty every step of the way in a transparent manner: one method for estimating square-roots, another for interpolation, and yet another non-mechanical exception step to generate an optimal final estimate for each value in the table. The Kerala Ganita experts extended such prior work to infinite series, including their own innovative exception terms [1].

Western mathematicians who reviewed Ramanujan’s notes found that he often used the terms “nearly” and “very nearly”[10]. Ramanujan came up with clever, non-mechanical approximations for specific quantities like π. Some of his approximations eventually lead to exact results. His exact infinite series for π triggered the most dramatic leap in accuracy since Madhava [14]. Some examples of his approximations are shown below [10].

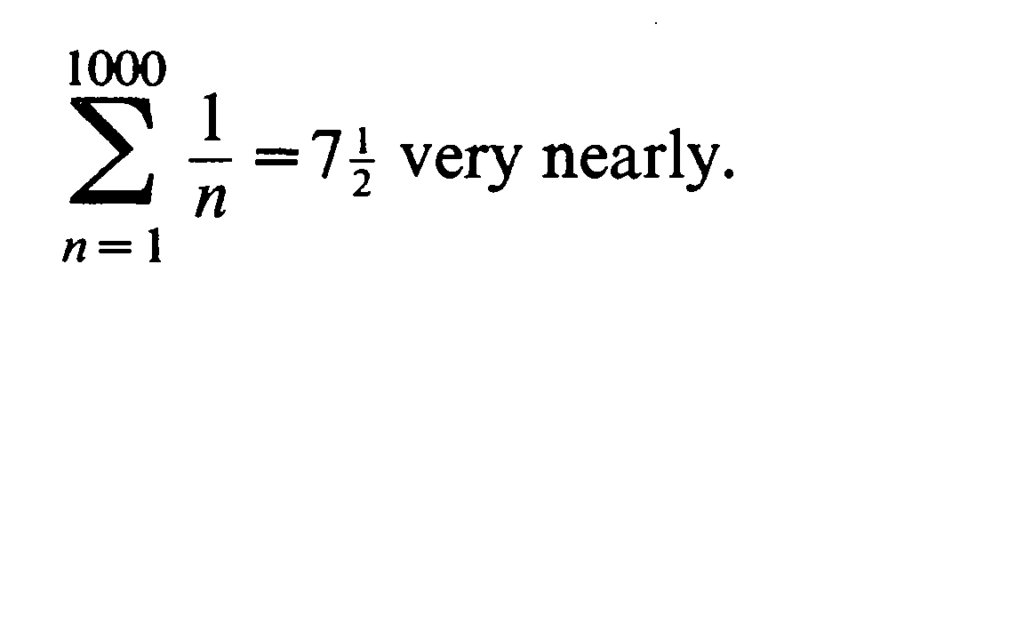
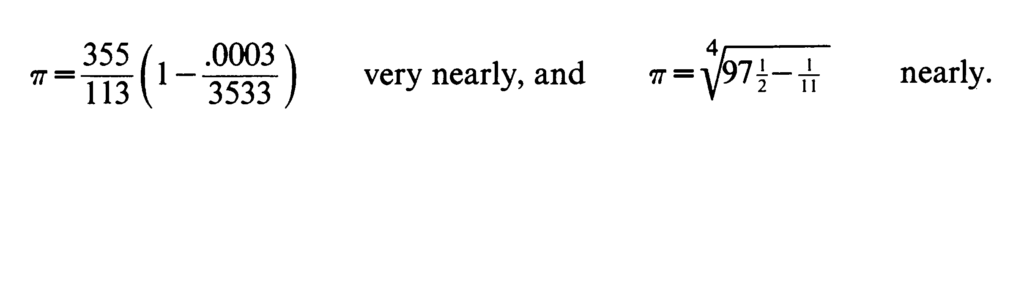
The Indian approach seeks balance between chaos and order [4] and represents a dharmic optimization under uncertainty.

Eliminating uncertainty and deleting Yukti, Upapatti, and Pramana from Ganita to digest it, drains it of key features that make it a powerful and reliable approach for solving real-life problems. Furthermore, lack of Pramana can lead to pseudo-science and fraud, as we will see shortly. Preserving these features within an Indian approach to Mathematics has the twin benefits of recovering pragmatism and making the subject understandable and usable by everyone. It protects against further digestion and denigration of the source tradition.

Finally, How can Ganita preserve this poison pill while continuing to retain its open architecture [13] and confidently exchange knowledge with other cultures?

The need of the hour is a thorough and systematic purva paksha of Mathematics and Modern Science, employing an Indian lens.

We don’t have to be a Manjul Bhargava to experience some differences between Ganita and Math.  We can simply try out the basic instruments employed within each subject.

Indian Rope vs Euclidean Geometry Box

One of C.K. Raju’s most important contributions is his cogent argument for a fundamental change in the way math is taught in Indian schools and colleges.

The rope is a key entity in Ganita and the Darshanas. A fundamental feature of the rope is its flexibility, reflecting the idea of ‘one manifesting as many’. The night-time confusion between a rope and a snake is an example that has been used Dharmic seekers to communicate the deep ideas about the nature of ultimate reality.

The knotted rope is a critical component of the ancient Indian navigational instrument known as the rapalagai  or kamal [1]. The ‘Sulba’ in the Sulba Sutras means ‘cord/string/rope’, and the rope served as a measuring tool since ancient times. Consequently, as C.K. Raju notes, the circumference can be the independent quantity measured quite naturally using a rope, with the straight line radius derived from this. A mathematical mind measures the straight line (Euclidean distance) first. A geometry box consists of an assortment of rigid straight-edged tools, and each one is used for a specific operation.

A knotted string can measured curved lines. When it is stretched taut between pins, it becomes a straight line, and with one of the pins freed, it behaves like a compass. This strings-and-pins set can be used to construct squares, rectangles, circles, etc, i.e., its flexibility reproduces the functionality of an expensive geometry box at a fraction of the cost. It unlocks the creativity of Ganita and is available even to the poorest student.

Indian Nyaya versus Aristotelian Logic

From the Indian point of view, two-valued (Aristotelian) logic can play a supporting role (e.g. like tarka [22]) but does not enable a person to attain a higher level of consciousness [4]. Note that such reductive logic is different from the holistic logic of Nyaya, which accepts multiple pramanas. In fact, no major school of Indian thought directly mentions deductive logic as pramana [22]. On the other hand, all major Indian schools of thought accept pratyaksha pramana, which in rejected by Mathematics [1]. Misusing two-valued logic (that has no place for uncertainty) as pramana negates Ganita’s poison pill.

Mathematics in India Today

The  current approach to teaching mathematics in India appears to be a stressful  and boring mixture of bits-and-pieces of Ganita mashed up with partially understood formal Mathematics imported from the west. This digested teaching approach has been successful in confounding multiple generations of Indian students. The modern rote/mechanical mode is a distortion of the original approach of recollective memory, which was a distinct mode of learning that cultivated the amazing computational (Ganita) abilities of the Indians [15].

Repeat after me:

“An acre is the area of a rectangle

whose length is one furlong

and whose width is one chain” – Pink Floyd, The Wall.

The 2016 Hindi movie ‘Nil Battey Sannata’ (~ 0/0) dramatizes this state of confusion. The movie claims that Math is a natural enemy of girls (“Ladkiyon ko Maths se purani dushmani hain“). While this may or may not be true,  the daughters of Lilavati  should not experience any difficulty with Ganita. For the great Shakuntala Devi, Ganita was a bandhu, not an enemy. The sophisticated Ganita within Kolam designs attests to the embodied learning capability within women. Let us also not forget the women engineers of ISRO who mastered the Ganita of rockets and spacecraft (yes, Ganita’s calculus without limits can do this well [1]).

The intrepid mother in the movie tells her daughter that “maths yaad karne ki nahi, samajne ki cheez hai“, while the maths-savvy classmate advises: “ek baar maths se dosti karke dekho, usse majhedaar aur kuch nahi“. A key scene in the movie shows everyday, familiar objects from real life being used to convey this ‘samaj’ – clearly a Ganita rather than an Euclidean solution to an Indian problem [15].

In formal math, even something as simple as a point (Bindu) gets hairy. (Euclid: A point is that which has no part, then graduate to this).  A blind import of western approaches into the Indian classroom without subjecting it to a thorough purva paksha,  is a folly not just restricted to Ganita, but one that been repeated in different areas of study including social sciences, economics, religion, art, etc. The net result is years of misery for most Indian students followed by a trip to the west to get it straight from the horse’s mouth. S. Gurumurthy has repeatedly noted the negative impact and the poor track record of such a reductive mathematics in solving practical problems in the Indian economic context.  We close with a discussion on contemporary mathematics and the way forward.

The Needham Question

"With the appearance on the scene of intensive studies of mathematics, science,  technology and medicine in the great non-European civilisations, debate is likely to sharpen, for the failure of China and India to give rise to distinctively modern science while being ahead of Europe for fourteen previous centuries is going to take some explaining” - Joseph Needham.

Many Indian scholars have attempted to answer this complex question. However, virtually all of these responses that try to provide social/religious explanations offer little insight due to a shallow understanding of dharma and Ganita traditions, and the inability to do a systematic Purva Paksha of the western approach using an Indian lens. We quickly summarize three perspectives below noting that we are only scratching the surface here.

A. Several centuries of foreign occupation

This occupation of India ranked among the worst and longest-running genocides in history and was characterized by violence that specifically the Indian intellectuals. Such a strategy is likely to have taken a heavy toll on Indian R&D output and institutions. When there was a sustained break from this violence, e.g., the time period of  the Vijayanagara empire,  we observe that Ganita, Ayurveda, astronomy, and other sciences achieved significant progress.

B. Civilizational inertia: complacency or weariness?

The sharpest debates in India occurred internally, between the various darshanas, which may have shifted the focus away from the study of external cultures entering India. There appears to be no evidence of a thorough study of the axiomatic approach from a native perspective. The Indians may have identified the lack of integral unity in the western approach and rejected it without any further examination of possible useful features.  CK Raju notes in [1] that it was only in the 18th century that India got the Elements translated from Persian into Sanskrit (by Jai Singh). This lack of a systematic Purva Paksha is not limited to Ganita alone but is also seen in many other areas, as pointed out by Rajiv Malhotra [16], suggesting an overly inward focus, careless disunity against an external threat, and a lack of strategic thinking.

C. The Unreasonable Effectiveness of Mathematics

Roddam Narasimha’s analysis examines a question complementary to Needham’s: what are the reasons for a sudden European resurgence after 1400+ years of backwardness in science and technology? He cites a key reason for their resurgence in the 17th century: the mathematization of science. Galileo is his study of the motion of falling bodies, used the calculus (via Cavalieri) to came up with the ‘law of the parabolic fall’. This is considered the first ever quantitative representation of motion using mathematical equations [12].  Scientists thereafter began to develop effective quantitative models relating different physical quantities like velocity, momentum, etc. using abstract models and calculus.Newton titled his famous scientific work as ‘Principia Mathematica‘. These mathematical models, however ‘wrong’ they may be, helped in new discoveries.

Indian Ganita experts too may not have anticipated this unreasonable effectiveness of mathematics when they rejected it for centuries. Narasimha summarizes this in [17]:  “Modern science seems to have acquired, perhaps by fortunate accident, the property that the great Buddhist philosopher Nagarjuna called prapakatva: i.e., it delivers what it promises; it may not be the Truth, but it is honest“.

The Road Ahead

Ganita, in the more recent interactions with modern science and math has made positive contributions, e.g., Satyendranath Bose and Narendra Karmarkar. The Bose-Einstein statistics comes out of counting exercise and is a significant contribution to Quantum Mechanics[17]. Karmarkar is famous for inventing the first practically effective algorithm for solving linear programs that is also theoretically efficient. Karmarkar’s proof of convergence demonstrates Yukti in gradually reducing the level of uncertainty in the solution quality in way that is both practically viable, and theoretically rigorous (a teeny bit of uncertainty remains in the end but it can be safely ignored).  Clearly, interacting with and exchanging ideas with other cultures can be beneficial, provided it is done with eyes wide open.  Scientists and applied mathematicians today employ a variety of different methods, including deduction, induction, inference, etc., along with empirical validation, etc., to come up with new findings and inventions.

Per Roddam Narasimha, the Indians paid a price for rejecting the axiomatic approach, but their stance was vindicated later by the 20th century developments in Quantum/Classical Mechanics and Logic [17].  Furthermore, modern science is being increasingly plagued by a variety of harmful ‘viruses’ that would not affect a ‘Ganita OS’.

Unreasonable expectations from Mathematics

The mathematization of science has succeeded, but only when the order it brings is honestly balanced by the reality check of an unpredictable nature.  The unbalanced mathematization of economics has resulted in a series of spectacular failures when applied in real life. Indian thinkers like S. Gurumurthy have studied these economic models in depth, and opted for a balanced Ganita-like method, bringing in empirical validation and Yukti to determine practical solutions anchored in Indian reality. Western social science, which mimics the axiomatic approach is degenerating into a self-serving pseudo-science that offers little insight. A sizable proportion of results published in modern scientific journals are not reproducible. This highly cited 2005 article discusses the implications.  And then there is the issue of fraud that is peculiar to the western modeling approach based on Aristotelian logic.

Falling for Supermodels

Supermodels sell an advertising pitch, not reality. Yet the temptation of falling for the perfection of abstract math models and ignoring the uncertainty of the real world can be too strong. As [17] notes: “The history of Western science is shot through with the idea of theories and models and of fraud. Ptolemy himself has been accused of fraud; so in more recent times have Galileo, Newton, Mendel, Millikan and a great variety of other less well-known figures. I believe the reason for this can be traced to faith in two-valued logic.” All models approximate reality. When this gap gets too wide, it makes sense to reject that model. However, it is tempting to reject reality in favor of a pet model or preferred hypothesis by cherry-picking data, fudging results, or tweaking the model in ‘creative’ ways to ‘make’ it work (e.g. some ‘AIT’ models in the Indian context).

Ganita does not suffer from this issue. Why? As noted in [17] that when “observation is the starting point and one has no great faith in any particular physical model, which was the prevailing norm of Indian scientific thought, the question of fraud does not arise. Indian scientists, even classical ones, do not appear to have accused each other of fraud. This could not have been mere politeness, as they did make charges of ignorance or even stupidity against each other (as Brahmagupta did on Aryabhata, for example). We could say that fraud is the besetting sin of a model-making scientific culture“.

Synthetic unity has its advantages and has revolutionized modern science, but progress based on Integral unity is more sustainable.

Some western scientists and mathematicians may have sensed this lack of Pramana. Poincare explored the role of intuition and inference in his candid 1905 essay [18]. We even get a hint of integral unity here. Albert Einstein was aware of the limitations of Math when he noted “As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.” Contemporary mathematician Terrence Tao recognizes that there is more to mathematics than just rigor and proof [19]. Thus, we see a limited move by Math toward the Ganita position while remaining firmly grounded in its native western tradition. Ganita can reciprocate in mutual respect, anchored in its own epistemology. We conclude with an informal discussion on emerging technologies.

Digestion by Machine: Math versus Ganita

Ganita is well-suited for this era of decentralized internet, analytics, big data, and digital computing which is algorithm driven. The emerging world of Artificial Intelligence is also very interesting. We touched upon AI citing an important observation of Subhash Kak [20] in our post on Ganita. As AI becomes highly sophisticated, it will be able to automate many human capabilities. It may eventually master the axiomatic approach and digest the Euclidean mathematician.

On the other hand the Indian approach to knowledge is rooted in the correspondence principle of Bandhu. Potential fallibility is acknowledged. Machines cannot replicate embodied knowing since they lack Bandhus, and they will not have the ability to attain a higher state of consciousness. For example, machines cannot chant mantras. Next, this ‘Euclidean’ robot will be able to master scriptures, and emulate all text-prescribed functionality of a cleric. It can function as a virtual holy establishment by delivering impeccable discourses. It will become an expert of theology by encoding history-centric truth claims as axioms and applying two-valued logic. However, it cannot become a Yogi.  Learning Ganita and internalizing the Dharmic worldview offers job security in the world of robots!  India can lead the way forward by carefully reintegrating useful features of modern science and math into its Vedic framework [21].

References:

1. Cultural foundations of mathematics: the nature of mathematical proof and the transmission of the calculus from India to Europe in the 16th c. CE, C. K. Raju. Pearson Longman, 2007.
2. Plato on Mathematics. MacTutor History of Mathematics archive. 2007.
3. Plato’s Theory of Recollection. Uploaded by Lorenzo Colombani. Academia.edu. 2013.
4. Being Different: An Indian Challenge to Western Universalism. Rajiv Malhotra. Harper Collins. 2011.
5. Axiomatism and Computational Positivism: Two Mathematical Cultures in Pursuit of Exact Sciences. Roddam Narasimha. Reprinted from Economic and Political Weekly, 2003.
6. Use and Misues of Logic. Donald Simanek. 1997.
7. Computers, mathematics education, and the alternative epistemology of the calculus in the Yuktibhasa. C. K. Raju. 2001.
8.  American Veda: From Emerson and the Beatles to Yoga and Meditation How Indian Spirituality Changed the West. Phil Goldberg. Random House LLC. 2010.
9. Logic in Indian Thought. Subhash Kak.
10. Ramanujan’s Notebooks. Bruce Berndt. Mathematics Magazine (51). 1978.
11. C. K. Raju. Teaching mathematics with a different philosophy. Part 2: Calculus without Limits. 2013.
12. Infinitesimal: How a Dangerous Mathematical Theory Shaped the Modern World. Amir Alexander. Farrar, Straus and Giroux reprint / Scientific American. 2014.
13. Indra’s Net: Defending Hinduism’s Philosophical Unity. Rajiv Malhotra. Harper Collins. 2011
14. Mathematics in India – From Vedic Period to Modern Times: Video Lecture Series, by M. D. Srinivas. K. Ramasubramaniam, M. S. Sriram. 2013.
15. Mathematics Education in India: Status and Outlook. Editors: R. Ramanujam, K. Subramaniam. Homi Bhabha Centre for Science Education, TIFR. 2012.
16. The Battle For Sanskrit. Rajiv Malhotra. Harper Collins. 2016.
17. Some thoughts on the Indian half of Needham question: Axioms, models and algorithms. Roddam Narasimha. Infinity Foundation. 2002.
18. Intuition and Logic in Mathematics. English Translation of Essay by Henri Poincaré. 1905.
19. The Pragnya Sutra: Aphorisms of Intuition. Subhash Kak. Baton Rouge, 2006.
20. There’s more to mathematics than rigour and proofs. Terence Tao. 2009.
21. Vedic Framework And Modern Science. Rajiv Malhotra. Swarajya Magazine. 2015.
22. Epistemology and Language in Indian Astronomy and Mathematics. Roddam Narasimha. Journal of Indian Philosophy, 2007.
23. The Math Page. Plane Geometry: An Adventure in Language and Logic based on
    Euclid’s Elements. Lawrence Spector, 2016.
24. Continuity and Infinitesimals. Stanford Encyclopedia of Philosophy. 2005, substantive revision 2013.
25. The Indian Origins of the Calculus and its Transmission to Europe Prior to Newton and Leibniz. Part II: Lessons for Mathematics Education. C. K. Raju, 2005.
26. Why Write: Legos, Power, and Control.  F. D. Poston. Johns Hopkins School of Education.
27. Indo-Portuguese Encounters: Journeys in Science, Technology, and Culture. Edited by Lokita Varadarajan. Indian National Science Academy. 2006.
28. The Kerala School, European Mathematics and Navigation. D. P. Agarwal. Infinity Foundation Mandala website.

Acknowledgments: I'm deeply grateful to the ICP blogger and editor for their constructive comments, review, and feedback.