Summary

Part-1 focused on the transcendental objective of the Sulba Sutras. Geometrical metaphors and algebraic ideas emerge from the system of correspondences (bandhus) established in the Yagna [3, 4, 5]. This results in a natural unity among seemingly diverse disciplines such as ganita/engineering and Indic art/architecture.

https://indicportal.orgsulba-sutras-the-indic-approach-to-engineering-1/

Geometrical Science and Engineering Principles 

This post is a limited-sample study of the engineering and geometrical principles discernible from the Harappan era through the Sulbasutra period. It is divided into two sections. It may be convenient to use the page jumps provided to navigate through this post.  As always, the references at the end will offer a more comprehensive view of these topics.

Section 1: Harappan Engineering

Section 2: Sulba Vijnana

Harappan Engineering

Although the Saraswati script is yet to reveal all its secrets, the Harappan constructions speak the universal language of Ganita.

In this section, we study how key structural engineering innovations of the Sindhu Saraswati Civilization emerge from kshetraganita. The Harappans made astounding progress in urban planning, sanitation, residential and public works, water resources management, and other areas. The excavations from that time period provide a snapshot of the state of Indic engineering in the 4th-3rd millennium BCE [15, 17].

We distill key points from Michel Danino’s talk at IIT-Madras and other references:

• Geometry of the Harappan Brick (~3000 BCE)
  • Some length-width-height ratios for bricks are preferable to others depending on the context. The dimensions adopted by Harappan brick-makers were simple and special and in a modern ratio of 1:2:4.
  • This brick geometry results in a structurally effective and economical bond. Summarizing his remarks, Danino states that their brickwork should be termed the Harappan bond rather than the English bond.
  • Multiple researchers have commented on the quality and design of these bricks.   K. N. Dikshit observed [23]: “the bricks used for the building of houses in Mohenjo Daro and Harappa are well burnt and of excellent proportions,  which have excited the admiration of modern engineers in Sind. The most usual size of burnt bricks is 11’’× 5 1/4” or 5 1/2” with a thickness of 2 1/4” to 2 3/4”.

• Highly polished and level stone segments as building blocks
  • Modularity: Bricks combine to form transverse elements. Highly polished and level stone column segments were combined into vertical pillars. Tapering may enhance stability and aesthetics. The column sections can be crafted elsewhere and easily transported to site and assembled as a pillar to the desired height.
  • Another theory cited in Danino’s talk that needs to be tested is that such segmented stone pillars may better resist earthquakes in a seismically active zone where un-reinforced brick masonry can be vulnerable.
  • Earthquake impact can be represented as a dynamic lateral acceleration  at the base of a structure. A rigid-body monolithic column would transmit the entire impact up to the rest of the structure whereas highly polished segmented sections can shift relative to each other.
• Harappan wells (~2600 BCE)
  • It is worth studying this example in some detail since this involves a remarkable breakthrough. In Mohenjodaro, the water table was known to be high. Underground infiltration generates pressure on the outside of the well-wall.
  • If regular bricks are used, the pressure on the underground brickwork (up to 20 meters deep) eventually triggers a collapse inward into the well [15, 18]. How did the Harappans solve this problem?
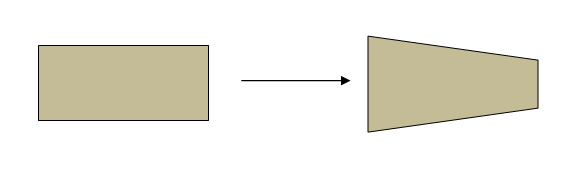
  • Bricks as structural elements perform well under a compression load. The ancient Indian engineers harnessed the brick’s compressive strength by altering the geometry of their bricks.

• • Employing trapezoidal bricks that taper inward results in a circular wall as shown in the picture below. Arch action is initiated by any external pressure and gets transmitted throughout the trapezoidal bricks as a compressive impact.
  • The bricks self-organize in harmony with their geometry and lock together, resulting in static equilibrium, and do not cave-in.
  • The degree of tapering and the well geometry are interrelated: If (R, r) is the outer and inner radius of the well, the altitude of the trapezoid is (R-r) and the ratio of the lengths of the parallel sides is r/R.
  • This circular-arch well that resists external water pressure is the earliest known example of the structurally true arch, which Prof. Danino notes, qualifies as an invention by Harappan hydro engineers.
  • There is no evidence yet that this invention was transposed by 90° to build true vertical arches to resist gravity load instead of water pressure. Mohenjodaro’s drains employed corbelled arches. 2000 years after the Harappans, the Roman engineers became famous for their use of vertical arches, and as Prof. Danino notes, they were unaware of this horizontal arch well innovation.
  • Additional structural innovations can also be seen in Harappan wells, suggesting a sound empirical understanding of engineering principles.

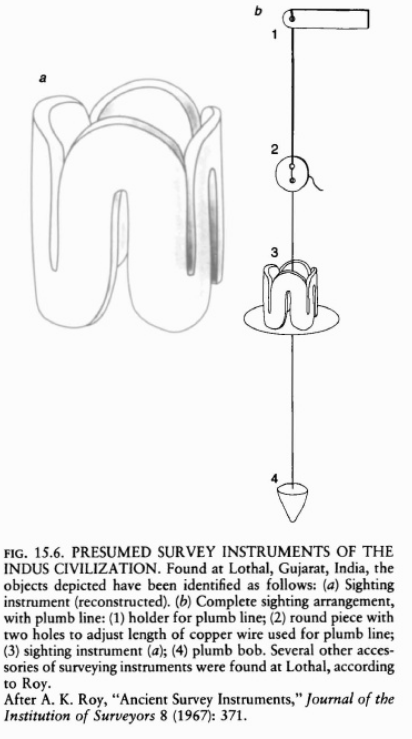
• The excavated urban plans, water drains, public baths, etc. at Lothal indicate the application of civil engineering instrumentation and geometrical methods for alignment and leveling. This is evidenced by several surveying instruments and accessories discovered at Lothal [21].

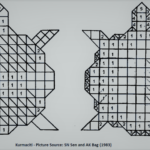
• Excavated pottery depict a series of regular shapes marked using geometrical instruments:  intersecting circles, squares, inverted triangles, etc. [2].

From Harappan Geometry to Sulba Sutras

We review several examples pertaining to Harappan units of measurement and proportions that persist through the Sulba time period and beyond.

• Urban Harappan house plans resemble those seen in rural India even today.
• Fundamental units of measurement:
  • An angula was 1.76 cm at Dholavira [15], and reported as 1.778 cm at Lothal.
    • The Sulbasutra also uses angula as a basic measurement unit for altar construction, and one estimate is 1.9 cm [20].
  • Harappan urban layouts yield an estimated unit of length of 1.9m [15], which is 108 times their angula.
    • 108 is a central Vedic number (e.g. 108 Karanas in the Natyasastra) and a number of Bandhus are associated with this number [4, 5].
    • The linear Purusha in the Sulbas is around 2 meters (2.28 m per Kulkarni [20]).
  • Harappans employed a unique decimal – binary system for their weights (not the decimal place value system of Ganita that includes 0) [15, 16].
  • 
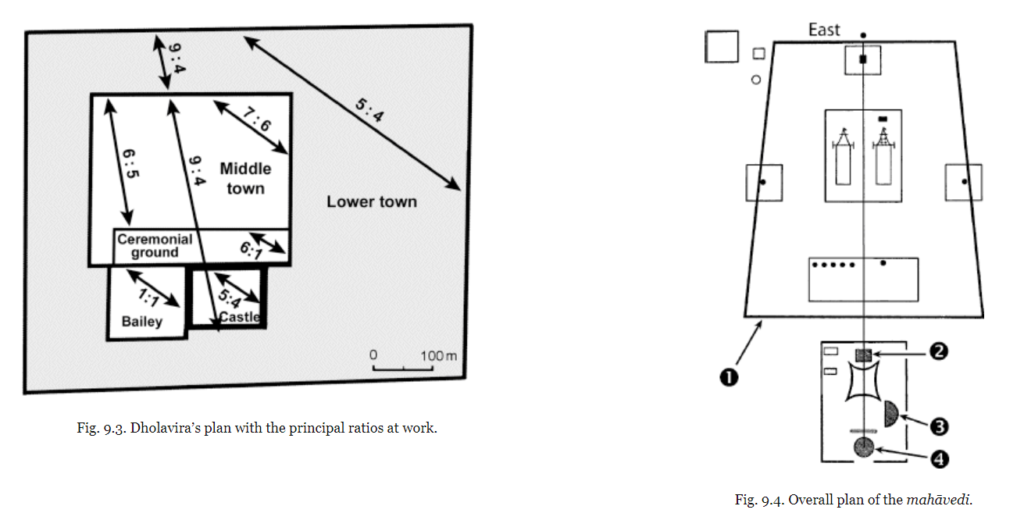
• The urban layout has streets organized at right angles along the cardinal directions. The Vedic altars are also oriented with respect to the E-W line (Praci).
• The repeated use of specific building ratios at Dholavira (5:4 and 9:4) are in consonance with the proportions used in the Sulba constructions [15].

• Similarity in the shapes of the Lothal altar and the Vedic Altars:

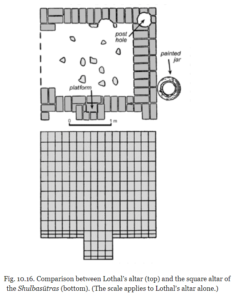
• The most common Harappan pottery motif, the rectangle with in-curved sides is preserved in the shape of the Vedic altars, including the important Mahavedi [2].
• Ceremonial structures like Vedic fire altars can be seen in Lothal and in Kalibangan, which were constructed in five layers of bricks [5].
• Astrophysicist J. McKim Malville is quoted [16] on the commonality in measurement principles that can be observed in Dholavira: “the apparent intent … to interweave, by means of geometry, the microcosm and the macrocosm”.

It is apparent from these findings that the Harappan constructions and methods indeed reflect an integral (Indic) approach to engineering that persisted long after their era.

"To the ancient mind, the concept of sacred space is inseparable from the practice of town-planning and architecture".
- Michel Danino [16].

Over time, this accumulated knowledge enabled the Indians to execute precision engineering projects that met stringent tolerances, satisfied structural stability requirements, showcased India’s unparalleled artistry, while always serving a primary transcendental objective. It took several centuries for the most destructive organized religions known to mankind to break down much of this sacred architecture. Despite their best efforts, some divine examples of Indic engineering survive.

Kailasanatha Mandir at Ellora “By Y.Shishido CC BY-SA 3.0, Link 

The Kailasanatha temple is architecture as well as sculpture. It is both cave and temple. “It is both natural, because it has not been built, as well as artistic, because [it is] gained by human effort of excavation“[27].  It is also an engineering masterpiece and represents “an excellent example of Reverse Engineering and was chiselled from top down … the temple has the largest cantilevered rock ceiling in the world. There was simply no margin of error here…” [26]. Beyond its sublime artistry and engineering wizardry, the Kailasanatha temple architecture’s overarching message is transcendental:  From the great Marathi saint Jnanadeva’s vision emerges a question for us [27] – Murti, mandir, and beings are sculpted out of the same mountain-rock, so which part of it (and the cosmos) is sacred space and which is not?

Sulba Vijnana

1. Vijnana and Modern Science
2. Units of Measurement and Terminology
3. Construction of Nityagni and Kamyagni
4. Square on the Diagonal Result
5. Combination, Transformation, Enlargement of Altars
6. Circling the Square, and Squaring the Circle
7. Geometric Algebra, Square Roots, and Fractions
8. Concluding Comments

Introduction

A knowledge of Ganita was required prior to studying the Sulbas, as affirmed by Sivadasa (between 1150 and 1320 CE) who wrote is his commentary on Maanava Sulba Sutras [1]: ‘the study of the Sulba should be begun after having finished the science of mathematics. Otherwise there cannot be a thorough knowledge of Sulba‘. Among other requirements, one must be comfortable working with fractions, the rule of three, approximations (calculating with ‘irrational’ numbers), and managing permutations and combinations.

Self-Verifying Computation versus Self-Evident Axioms

Per Bibhutibhushan Datta, the earliest Hindu name for geometrical sciences was Sulba Vijnana [1]. Saraswati Amma mentions how this field later became part of the Ganita family as kshetraganita alongside Paatiganita (arithmetic) and Bijaganita (algebra) with Jyotisha covering all branches of Ganita [2], which eventually included the calculus of the Aryabhata school of Kerala. The calculations of volumes for earth-moving (excavations) were covered in Khatavyavahara while Rasiganita, which dealt with the calculations relating to heaps, also included geometrical aspects [2].  

Datta refers to Vijnana as a science in the Sulba context [1]. When we refer to ‘geometry’ in the Indian context, we do so using the Indic perspective, and not ‘Euclidean geometry’ that made its entry later. Sulba Vijnana’s validation of stated propositions are not through the western approach of theorems-and-deductive-proof based on self-evident axioms, but through demonstrations and constructions. This important point was stated by Bibhutibhushan Datta more than 80 years ago [1]. This approach is consistently followed in Ganita through the ages.

Vijnana and Ganita are Sanskrit non-translatables having multiple context-dependent meanings and cannot be limited to modern science and mathematics. Western science too rejects claims that disagree with experiment, but differs from vijnana: the latter is rooted in a Vedic cosmology that is free of the tension of the religion-science-mathematics fragmentations. Sulba vijnana in its Yagna context points to an integral knowledge and an experiential understanding that emerges from consciousness.  Through prayoga a practitioner can simultaneously test a claim as well as realize the truth, reflecting the maxim: “doing is the best way of knowing and learning“ [19]. The self-verifying constructions in the Sulbas seem to be in consonance with the self-organizing cosmos (a manifestation of ritam [4]) of the Rig Veda.

"The spider that extrudes its own web without any extraneous agency is proffered as a metaphor for Brahman as both the efficient and material cause of the universe".
  - Rajiv Malhotra in 'Being Different' [4].

This unity of computation & verification in Ganita is also mentioned in the Aryabhatiya.

Ganita Lec-8. Aryabhatiya part-2: http://t.co/7QIzQgV7Uv
interesting verse. dual use: computation + verification pic.twitter.com/NSsTvKupNn

— Shivoham (@Ganitamrita) December 13, 2014

Saraswati Amma identifies 3 categories of such geometrical knowledge in the Sulbas:

a) Results that are explicitly stated,

b) Constructions, and

c) Geometrical truths implicit in the constructions.

Geometry in the Sulbas was primarily constructive in nature [2] although we do find some demonstrations of the geometrical results in the later Sulbas (e.g., Katyayana’s Sulbasutra) [1].  Saraswati Amma’s work [2] has to be acknowledged for recognizing the transcendental objective of the Sulbas. She has explained how this Vedic approach shaped the methods of preservation and transmission of Ganita knowledge in India through the generations: The main works, often through sutras, enunciate the procedures required for proper altar construction and performance of Yagnas. Thereafter, the technical derivations were likely to be present in commentaries, and the rationale of the great teachers were transmitted orally, similar to the practice in Ayurveda. We see this resemblance with Ayurveda in Sulba terminology as well.

Units of Measurement and Terminology

Measurement

Sulba primarily means measurement. Measurements were done using the measuring tape called the Rajju, although sometimes Sulba and Rajju are used interchangeably. There is also mention of the bamboo rod (‘Venu’), which appears to have been gradually replaced by the Rajju. The measuring cord had to be smooth and of even cross-section throughout.  It was fabricated using sama (kind of hemp), balvaja (Indian goosegrass), munja grass, and kusa grass to make it strong and retain its elasticity after repeated stretching, and produce consistent measurements [25].

The Vedic Samhitas and Brahmanas stipulate rules of conduct for those engaged in altar construction [1]. To see what can happen when ethical considerations are set aside, consider this example [23]:

“We may cite an example from recent past to show how poor peasants were exploited by the land surveyors during the Mughal rule in India. In the seventeenth century, ropes made of hemp were usually employed for measuring and assessing land. Now, the hemp rope would shrink when wet and lengthen when dry. The government officials used to keep the rope wet on all sorts of pretexts… Later on the hemp rope was replaced by the more accurate bamboo rod with iron rings.”

When dharma took a backseat, trust in the contextually flexible and versatile Rajju was lost and people returned to a rigid and inflexible ruler.

Units of Measurement

Units of measurement used in the Baudhayana Sulbasutras [5]:

small pada = 10 angulas

pradesa = 12 angulas

pada = 15 angulas

aratni = 24 angulas

prakrama = 30 angulas

yuga = 86 angulas

vyayama = 96 angulas

aksa = 104 angulas

vyama = 120 angulas

(linear) purusa = 120 angulas

Purusa was also used as a unit for measuring areas and the Sulbasutras mentions three kinds of measures — one, two, and three dimensional.

Those who have lived in engineering campuses may recall seeing Civil Engineering students dragging metal linked chains for surveying. This practice probably goes back to the Harappan period [16]. Measurements for the Vedic Yagna were done by a sama-sutra-niranchaka, the uniform rope stretcher, or the Rajju grahaka (Pali), who was the king’s land surveyor. In later Silpasastra texts, the surveyor was called the sutra grahi or sutra-dhara who was also an expert in alignment [1]. A sutragrahi can refer to a Chief Engineer, and is a meaningful and historically apt choice given this connection to Sulba Sutras, the oldest known reference text for Indic Engineering.

Not taking sides in the debate on whether Baahubali was a civil or mechanical engineer, we include other engineering terms:

Yaantrika or Yantra-nirmana vidya — engineering (from Vaastu sastra)

Yantrakaara/Abhiyanta — engineer (M), abhiyantri (F)

Tantraagna — technician/technologist.

Indic terminology employs meaningful words that along with their root sounds reveal their Ganita qualities. This is possible because of the power of Sanskrit, as Rajiv Malhotra [4] notes: “Since every root sound has a distinct meaning, its signature is found in all the words derived from it. It is theoretically possible to explain the meaning of the words according to the algebraic combination of letters, syllables and roots… Naming was inseparable from realizing its essence. In Ayurveda, the names allow us to understand not only the morphological characteristics of a plant but also its medicinal properties.” Barring a few exceptions, the meaningful nomenclature of the Sulbas persisted in Ganita works through the ages [2].

Bibhutibhushan Datta (Swami Vidyaranya) and Saraswati Amma were Sanskrit scholars in addition to their mathematical expertise. They were capable of accessing and interpreting primary source content, and set many a record right.

Terminology

A sample list of terms used in the Sulba Sutras are given below and one can find an exhaustive list within [1, 2, 22]. It is possible that multiple Sanskrit words may be used in different Indic texts to describe a geometric figure or Ganita operation depending on the context and audience.

Closed Figure — Kshetra

Area — Bhumi, Kshetra

One-dimension

Line of symmetry of an altar — Prsthyaa

East-west (eastward line) direction — Praci

Perpendicular (north-south) — Tiryanmaani

Line —  Lekha or Rekha

Straight line — Rju-lekha

 

Two-dimensions

Square

Square — Chaturasra/Samachaturasra

Unit Square (to compute area) — Varga

Square of any number — Kriti, Varga

Side of the square, square root — Karani

(karani ~ producer, kriti ~ produced)

√2 — Dvikarani

√3 — Trikarani

Geometrical representation of a square number — Vargakshetra

 

Rectangle

Rectangle — Dirgha chaturasra

Geometrical representation of a product of two quantities — Ghaatakshetra

Diagonal (that which goes transversely) — Aksnaya

Two Sides — Tiryanmaani, Parsvamaani

 

Triangle

Triangle — Tryasra

Isosceles Triangle — Prauga

Altitude of triangle — Isu

Rhombus (double isosceles triangle) — Ubhyatah Prauga

Isosceles Trapezium (shorter in the front) — Purastaad Amhiyasi

 

Some Composite Fractions

⅜ — Triastama

2⁄7 — Dvisaptama

The terminology here is important because the name contains within it the ‘concrete concept of the operation of measuring’. Sanskrit allows us to recursively express fractions of fractions [1].

Circle

Circle — Mandala/Parimandala

Circumference — Parinaaha

Diameter — Viskambha, Vyaasa

Center/midpoint — Madhya

 

Fundamental Operations in Sulba constructions [1].

Addition (“putting together”) — Samaasa

Subtraction — Nirhaara

Remainder — Sesa

Division — Bhaaga, Vibhaaga

Replication (repeated operations) — Abhyaasa

Repeated enlargement — Vidhaabhyaasa

Finding Cardinal Directions

The east-west line (Praci) was established using the Sanku as explained by Prof. K. Ramasubramanian (see below) in the Q&A session at the end of the lecture. This approach is simple and free of instrumentation error.

Geometrical Constructions

Broadly, there are two types of agnis discussed in the Sulbas – nityagni and kamyagni.  The three primary Nitya Agnis are Garhapatya (circle), Ahavaniya (square) and Dakshina (semicircular) [1, 3]. The construction consists of five layers of bricks with each citi built up using a specific number of bricks of specific shapes. The Sulbasutras present the complete specifications required for precise construction. These specs are from prior works and much of the matter is traceable to earlier Brahmana and Samhita works.

Nityagni Constructions

Constructing the three nityagnis require the ability [1] to:

• Construct the perpendicular bisector to a given line
• Construct a square on a given line
• Circle a square, and vice versa
• Double a circle

This in turn requires two kinds of subject expertise that are listed below:

• Ganita Sastra: For an accurate approximation of √2.
• Sulba Vijnana: The area of the square on diagonal of any given square is double the area of that square. This is a special case of the more famous result discussed below.

Kamyagni Constructions

The second level of complexity is the construction of rectangular and isosceles trapezoidal figures. At the higher end of complexity are the kamyagnis, whose area, regardless of shape is fixed at 7½ purusas (108,000 sq. angulas [5]). This requires the ability to enlarge, shrink, rotate, and transform squares, triangles, and rhombuses. Several geometrical facts are implicit in the constructions [2]. For example:

• a) the circle is the locus of points at a constant distance from a given point.
• b) the perpendicular bisector is the locus of points equidistant from the two extremities of the line.
• c) the line connecting the vertex of an isosceles triangle to the mid-point of its base is perpendicular to the base.
• d) the tangent to a circle is perpendicular to the radius at the point where they meet.

We now discuss the fundamental proposition of geometry that was first discovered and used in many altar constructions.

Square on the Diagonal (SQD) Result

This famous and important result had a deep influence on ancient Indian geometry, trigonometry (e.g., sine-table), algebra, and perhaps Ganitasastra itself [2].  The SQD result was popularized by the western world and accepted by secular India as the Pythagoras Theorem. The Babylonians too are known to have stated some Pythagorean numbers but “the full geometrical significance of the theorem, that the sides of any right-angled triangle will exhibit this relationship among them, was first realized by altar-building Vedic priests” [1].

In the Ganita context, knowing Pythagorean numbers is insufficient, and an Euclidean-type deductive proof is neither necessary nor sufficient.

Since the Sulba does not speak of the right triangle (hence no hypotenuse is mentioned), the result is first stated by Baudhayana with respect to the square:

“the diagonal of a square produces an area twice as much“.

and later, he stated the general SQD result:

“the diagonal of a rectangle produces both (areas) which its length and width produce separately“.

On the other hand, later Sulba authors  state the general result first and then the special case, which indicates that over time, the generality of SQD was recognized [1].

As far as “proof”, there is no none in the Euclidean sense, although the constructions for which the result has to be known confirm that the Indians were well aware of the general applicability of the SQD rule. To know how old the result is, one has to find the most ancient mentions of its applications.

How old are the Geometrical Results in the Sulba Sutras?

"India's sands were never so kind to her records as Babylonia's sands have been to her clay tablets" - Saraswati Amma.

There is epistemological and other evidence regarding the knowledge of these geometrical results in the Rig Veda itself:

1. There are many reference to Yagna and fire altars in the Rig Veda.
2. The 3 places of the (nitya) agni are mentioned in Rig Veda Samhita.
3. Given the importance of the correspondence principle (Bandhu) in the Rig Veda, it is likely that the task of squaring a circle, and the special case of SQD is as old as the Rig Veda itself.

The first clear mention of the area of Garhapatya circle and Ahavaniya square of the same size is in the Satapatha Brahmana. Therefore, the science of altar construction likely dates back to the Brahmana and as early as Taittiriya Samhita [1]. The SQD result appears to have been used in the Satapatha Brahmana, but the proposition is stated only in the Srauta Sutras. We summarize the observations of Datta [1] regarding the SQD result.

• The Hindus recognized the geometrical nature of the result and put it to good use, and applied it to rectangles, the lengths of whose sides were irrational (e.g., for the construction of Sautraamaniki Vedi, Asvamedhiki Vedi).
• The Sulba author mentions after stating the SQD: ‘iti kshetrajnanam‘.  Kshetra in this context means figure, not area.
• Empirically, by constructing the squares on the sides and diagonal, and dividing them into unit squares, one can verify the result for any rectangle.

• 

• The special SQD case of squares is required in Baudhayana’s method to transform a square into a rectangle, where it is necessary to construct a square whose corners are turned toward the four cardinal directions.
• For geometric constructions of √2, √3, etc., SQD is ‘indispensable’.
• In Baudhayana’s Sulbasutras, the converse of the proposition is used to construct a Mahavedi. The converse of SQD is implicit in the text but is not explicitly stated.

Rational Rectangles

Did the ancient Hindus identify a general rule to find a limitless number of rational rectangles (~rational right triangles)?

To answer this, Datta quotes two verses from Apastamba Sulba:
1. Etaavanti Jneyani Vedi-Viharanaani Bhavanti.
2. Taabhir Jneyaabhiruktam Viharanam.

Jneya: it is known, from prior (Vedic) works; these are but the methods of constructions of the Vedi which are known from prior (Vedic) works [1].

The question is then answered in the affirmative. Saraswati Amma [2] remarks that the Sulba authors had ‘a genius for generalizing’, citing Katyayana’s general rule for combining squares as an example, and that they were familiar with multiple general formulas for finding the sides of rational right triangles. The ancient Hindus knew that new rational rectangles are obtained by multiplying or dividing sides and the diagonal by any rational quantity, and Apastamba has derived it this way [1].

We see several rational right triangles in the Mahavedi layout [24] where the diagonal is 1 + greater side, 2 + greater side, etc. Datta derives two equivalent general rules ‘A’ and ‘B’ for generating such triangles:

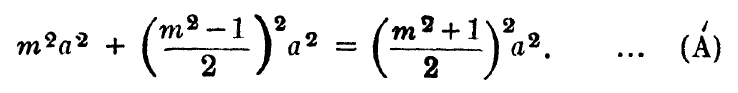
Rule ‘A’ with odd ‘m’ (3, 5, 7, ..) generates several rational rectangles stated in the Sulba such a (3, 4, 5) to (7, 24, 25), and rational rectangles where this difference is 2 can be generated by the following rule ‘B’ obtained by setting a = 2, m > 2 in (A).

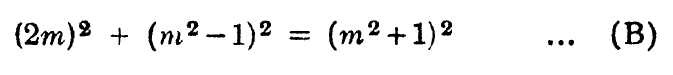
An important right triangle (15, 36, 39) in given in the Taittiriya Samhita, where the diagonal is 3 + the greater side. Baudhayana Sulbasutras specifically calls out this result. This instance was employed in the most ancient method of constructing the Mahavedi, and was considered sacred by tradition [1].

In [24], Parameshwaran, a scholar of Vedic mathematics, has commented on the sacred geometry of the Mahavedi and the importance in Vedic Yagna of the eastward striving aspect represented by the tapering of the trapezoid.

Sample Results and Propositions in the Sulbas

We briefly discuss two of the basic constructions in the Sulbasutras. For brevity, we refer to the video lecture of Prof. Ramasubramanian and present only the pictures of the final constructions.

Perpendicular Bisector (‘Fish Figure’)

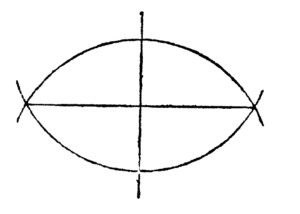
Constructing a Square Given a Side

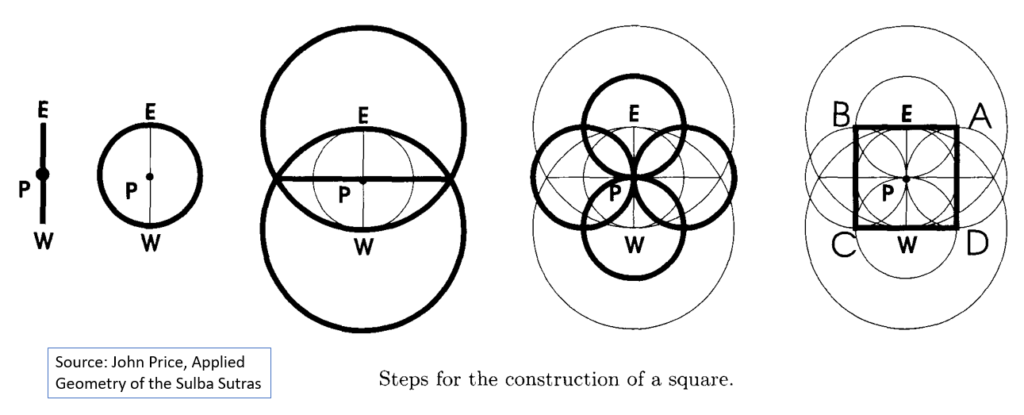
Examples of Combination of Areas

Part-2 of the video lecture covers the constructions involving combinations and transformations of squares and rectangles.

1. A1 = nA2. The SQD result is used here.
A special case occurs when n is a perfect square = p². The 2D task is skillfully reduced to a linear problem: construct a straight-line that is p times a side of the given square A2 and use that as the side of square A1.

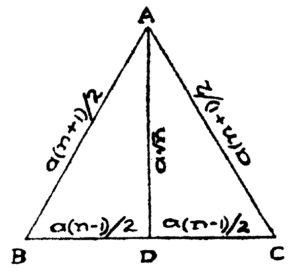
Elegant and simple methods are given for finding a square equal to a number of other squares of the same size [1]. For example, by constructing the isosceles triangle shown below using the specified base and side and applying the SQD result,

[a(n+1)/2]²-[a(n-1)/2]² = na²

i.e., the constructed altitude (Isu) will give the side of the required square A1 for any positive integer n (>1) and area a of square A2. The statement from Katyayana Sulbasutras is shown below.

2. A1 = 1/n A2.
A special case occurs when n is a perfect square = p². The 2D task reduces to a linear problem of dividing a side of square-2 into p equal parts. A1 is obtained by constructing a square using one of these line segments as its side.

3. A1 = A2 + A3 (construct square-1 whose area is the sum of the areas of two other different squares 2 and 3).

Baudhayana’s procedure based on SQD is simple and elegant: “cut off from the larger square-2, a rectangular portion having the side of square-3. The diagonal of this segment will be a side of the square having area (A2+A3)“.

4. A1 = A2 – A3 (construct a square whose area is the difference of the areas of two other different squares).

Apastamba has given a demonstration along with an example [1].

Examples of Transformation of Areas

1. Transforming a Rectangle into a Square [1]

An interesting step in the construction consists of chopping off (or making a copy of) the ‘flat’ rectangle (ABHG), rotating it clockwise by 90-degrees, moving it, and pasting it along the vertical line segment DF in the position DFH’G’.

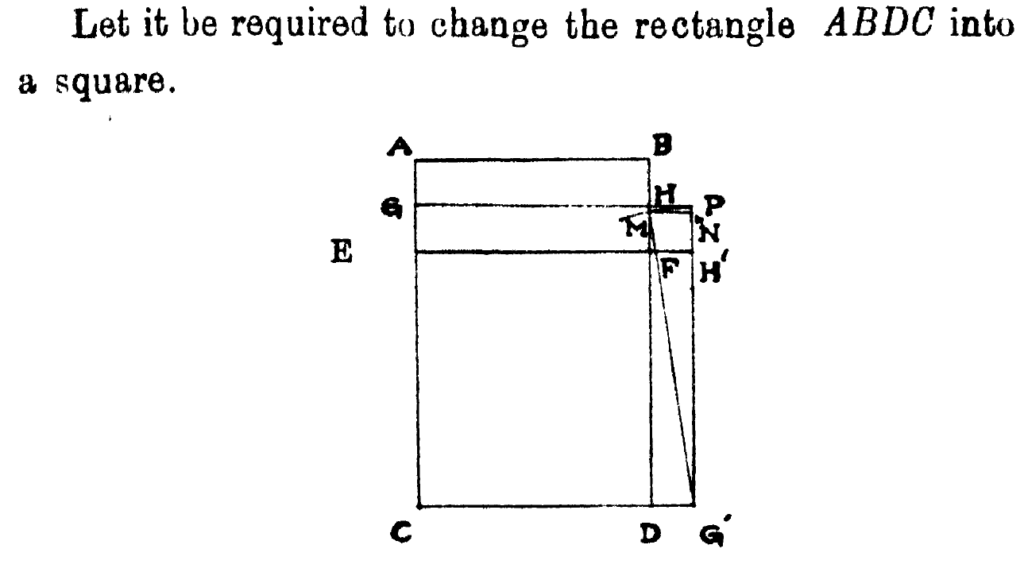
2. Transforming a Square into a Rectangle.

3. Transforming a Square or Rectangle into a Triangle or Rhombus.

4. Special construction: Construct a square of area 108 padas, i.e., whose area is thrice that of a square of side 6.

Note:

Sometimes, the cubic content has to be kept intact for two altars of different heights. Here, one obtains an approximation formula for the volume of a frustum of a pyramid (see picture below).

 

By MarinaVladivostok, CC0, Link

Scalability: Enlargement or Reduction of Altar Size

An important astronomical discovery emerges from the need to preserve the integral unity of successive (annual) enlargements of certain kamyagni altars by an area increment of one Purusa. The sequence of areas will be: 7½, 8½, …, 101½ Purushas, with the final construction 14X the area of the first altar. The shape and proportions within the altar have to be strictly maintained. Datta [1] shares the reason for this stipulation given in the Katyayana Sulbasutra:

The following correspondences are established in the Yagna: agni = Prajapati, his child is the unit of measure employed, and the womb is his unmanifest form, and therefore the spatial relations of that form must be preserved.

This altar construction cycle corresponds to the 95-year Yagnavalkya cycle of astronomy [5].

Engineering this design requirement is non-trivial, and requires one to solve the geometrical problem of constructing similar figures. The shape of these altars can be pretty complex and such constructions require a clear understanding of the relationship between length and area (“agni = Prajapati, and his child is the unit of measure employed”). It is observed by the Sulba authors that the number of square units in the area of a square is obtained by multiplying the number of linear units by itself. This was stated by Apastamba and Katyayana. Conversely, the length varies as the square root of the area. Using this correspondence, the Sulbakaaras came up with an ingenious design solution, which is also present in the Satapatha Brahmana.

Increase or decrease the length of the unit of measure in the ratio of the square root of the areas, but do not alter the number of units used in the construction.

To engineer a 14-fold altar enlargement, knowledge of the SQD result is essential [1] and was likely known and used before the Sulbasutra was codified. The resultant constructive algorithm (Abhiyukti) can be employed to enlarge an altar of area 7½ Purusa to (7½+m) Purusas, where m is a positive integer:

1. Make the incremental excess area (m) into a square or rectangle
2. Divide the resultant square/rectangle into 15 equal parts (m/15).
3. Two such parts are turned into a square (area = 2m/15) and combined with a square of one Purusa to generate a new square (area = 1 + 2m/15)
4. The side of this new square = √(1+2m/15) will be the new unit linear measure, which will preserve the proportions of the original Agni.

Applying this to scale up the final altar (m = 101-7 = 94), which is ~14X the area of the original altar, the new linear unit will ~√14 times the original measure.

Circling the Square

Baudhayana’s method of transforming a given square of side ‘2a’ into a circle having approximately the same area:

"if you wish to circle a square (ABCD), draw 1/2 its diagonal (a/√2) about the center towards the East-West line (EW); then describe a circle together with 1/3 of that which lies outside the circle (radius OP = OM + MP)".

Datta mentions the key phrase employed by Apastamba regarding this method:

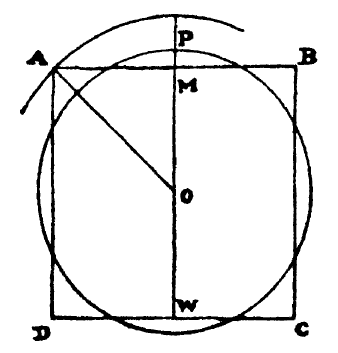
"saanitya mandalam:yaavadd hiyate taavad aagantu".

The prescribed procedure is an inexact (anitya) method of construction by “as much the circle falls short, so much comes in” [1]. The radius of the resultant circle r = a/3(2 + √2), yields a slightly larger area compared to the square, which can be checked empirically:
Area ~ 4.069 a², compared to the true area of square = 4a², using the famous √2 value given in the Sulbas.

Excess error ~ 1.72% < 2%

Squaring the Circle

Given a circle of diameter ‘d’, construct a square of equal area. A numerical solution is provided to obtain the length of the side of the square to be constructed.

"Divide the diameter (d) into 8 parts. then divide 1 part into 29 parts and leave out 28; also, the 6th part of the preceding sub-division less the 8th part of the last".

These steps yield the following finite series approximation for the side ‘2a’ of the resultant square [1]:

2a = d – d/8 + d/8.29 – d/8.29.6 + d/8.29.6.8

Computing an error bound:

2a = 1224/1393 d ⇒a = 0.43934d
⇒ error = (4*(0.5*1224/1393)^2 – 0.78539816339)/0.78539816339
area of circle = πd²/4 ~ 0.78539816339 d²
area of the square ~ 0.77207697806 d², i.e.  a slightly smaller square.

error ~ 1.697% < 2%

These constructions imply the following approximations for π [1]:

• π = 3.0885
• Maanava Sulba calculations yield π ~ 3.16049.
• Dvarakanatha, one of the commentators, improved the approximation to 3.158.

Ramanujan’s Solutions to Squaring the Circle

The squaring of the circle has a colorful history in Europe due to anxiety over the uncertainty injected by ‘irrational’ numbers. Ramanujan’s numerical contributions are well-known and in line with Ganita tradition. Here, he has contributed to a basic Sulba construction of squaring the circle. He does so using an approximate geometrical construction that is in the spirit of the Sulbasutra approach. The picture in his manuscript shows his 1913 solution that corresponds to a value of π ~355/113, which is accurate to 6 decimal places, the best at the time in the context of this problem.

By Srinivasa Ramanujan; verwendet von Petrus3743 – Who Was Ramanujan? von Stephen Wolfram, Public Domain, Link

In 1914, Ramanujan improved upon his own result using another construction (animation shown below) corresponding to an 8-digit accuracy of π.

The resultant error is minuscule: if we squared the ‘circular’ earth (radius ~6371 km) using Ramanujan’s construction, the error in the side of the slightly smaller square would be around 2 mm.

Origin of Geometric Algebra

Datta remarks on the algebraic significance of the geometrical constructions, noting that they form the seed of Geometrical Algebra which can be seen even in the Bijaganita of Bhaskara-2 (1114 CE). Some algebraic equations that emerge are listed below.

ax² = c (enlargement with equal proportions). The equation x² = 1+2m/15 can be derived from the m-th enlargement of the falcon-shaped (Syena) fire-altar.

ax² + bx = c (enlargement with increment)

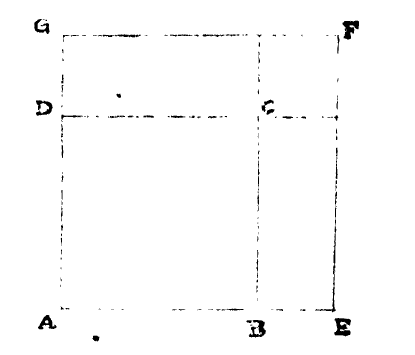
The geometric analog of the algebraic identity
 (a+b)² = a² + b² + 2ab

is obtained from the general rule for enlarging a square ABCD to square AEFG shown below.

If a = AB, b = BE, then (a+b)² = Area (AEFG) = sum of the areas of the two squares plus the twice the area of the equal-sized rectangles.

Square Roots (√2)

The following is the Sulba approximation for √2:

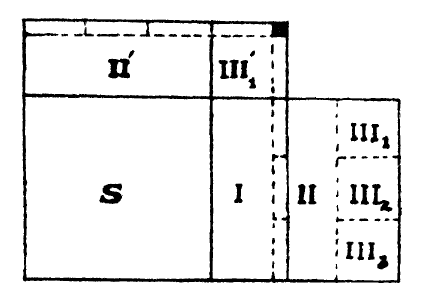
Its decimal value ~1.414216, accurate to five decimal places. Commentator Rama Bajapeya added a corrective pair of terms to improve accuracy to 7 decimal places [1]. How did the Sulba authors derive this series? Many interesting explanations have been given. Datta’s appears to be the best among those offered [1] and is an entirely geometrical reconstruction similar to those employed by Sulba authors. It starts with two squares having unit length, and involves the slicing of rectangular strips, rotating and pasting them, dividing areas into several equal parts, adding and subtracting areas, etc.

Datta uses this approach to approximate √3 ~ 1.732051 up to 5 decimal places.

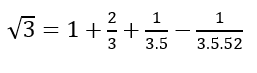
Commentator Kapardiswami noted the persistent inexactness in calculating √2: “in any case there will be an excess even by a fraction of the smallest part of the minute nivaara grain falling from the mouth of a parrot” (a vivid epsilon!). The commentaries of Kapardiswami and Karavindaswami imply the following knowledge in ancient India about their estimate of √2 that it was: a) approximate, b) an over-estimate, and c) cannot be completely eliminated. Datta shows that the meaning of the term ‘visesha‘ and ‘savisesha‘ have been correctly interpreted by the commentators.  The canonical texts of the Jainas (Suryaprajnapati, 500 BCE) uses visesha in the same way. Similarly, the Jambudviparajnapti (~300BCE) uses visesha to refer to a small quantity that has not been recorded and cannot be accurately determined, but has to be added or subtracted from the estimate in order to obtain its exact value. Nemichandra (975 CE) uses the term savisesha in exactly the same way as the Sulbasutras (tiny overestimate).

Fractions

How does one grasp the reality that the area of a square of side ½ is ¼ square units? Saraswati Amma [2] remarks on the Sulba author’s “unerring grasp of the area produced by fractional units of length, which is infinitely more difficult to conceive“. She quotes Apastamba who says that a cord of 1½ units produces 2¼ units of area, a cord of length 2½ produces 6¼ units of area; ½ a unit produces ¼, and ⅓ of a unit produces ⅑, based on a neat empirical observation: ½ of 2 units (= 1) fills up one quarter of the area (¼ of 4).

Complex Fire-Altars

For certain altars, the total number of bricks to be used in a layer are specified, but not their dimensions. We will get into this and advanced Sulba engineering topics in Part-3.

Summary

Editor’s Note: After all this discussion of Sulba sutras and Squares, Abhiyukti and Arches, there is one takeaway to remember: Indic Engineering is about more than just about holding up bricks, it is about upholding spiritual harmony between the mathematical and practical, the artificial and natural, the human and divine. Ayodhya isn’t only about rebuilding one destroyed temple. Ramarajya is to be experienced by reclaiming Bharata’s sacred space, both outer and inner, where bhavya Ram Mandirs mirror a billion मन Mandirs.

Dharyate anena iti dharmah — that which upholds [Rta] is Dharma.

References

(Partial list only. Full list will be shared along with Part-3).

1. Bibhutibhushan Datta (Swami Vidyaranya). The Science Of The Sulba: A Study In Early Hindu Geometry. University of Calcutta. 1932.
2. Saraswati Amma. Geometry in Ancient and Medieval India. Motilal Banarsidass Publishers. 1979.
3. Kapila Vatsyayan. The Square and the Circle of the Indian Arts. Abhinav Publications. 1997.
4. Rajiv Malhotra. Being Different: An Indian Challenge to Western Universalism. Harper Collins. 2011.
5. Subhash Kak. The Astronomical Code of the Ṛgveda (Third Edition). 2011.
6. Rajiv Malhotra. Indra’s Net: Defending Hinduism’s Philosophical Unity. Harper Collins. 2014.
7. Kosla Vepa. The Origins of Astronomy, The Calendar, and Time (Second Edition). 2010.
8. Prakruti Prativadi. Rasas in Bharatanatyam: First in a Series on Indian Aesthetics and Bharatanatyam. Creative Space. 2017.
9. N.R.I Pathi. Dharmic Development. Andhra Cultural Portal. 2014.
10. Prakruti Prativadi. The Bharatanāṭyaṃ Yajña. Swadeshi Indology-3 Information Handout. 2017.
11. Dharampal. Collected Writings in 5 Volumes. Other India Press. 2000.
12. John Price. Applied Geometry of the Sulba Sutras. Department of Mathematics, Maharishi University of Management, Iowa. 2000.
13. Amartya Kumar Dutta. Was There Sophisticated Mathematics During Vedic Age? in ‘An anthology of disparate thoughts at a popular level‘. ISIREA, Kolkata, 2016.
14. K. Ramasubramanian. The Origin and Growth of Mathematics in India. R C Gupta Award Lecture, IIT Bombay. 2010.
15. Michel Danino. Lost River: On The Trail of the Sarasvati.  Penguin Books. 2010.
16. Michel Danino. New Insights into Harappan Town-Planning, Proportions and Units, with Special Reference to Dholavira. Man and Environment (33). 2008.
17. Rima Hooja. Channeling Nature: Hydraulics, Traditional Knowledge Systems, And Water Resource Management in India – A Historical Perspective.
18. Michael Jansen. Mohenjo-Daro, Indus Valley Civilization: Water Supply and Water Use in One of the Largest Bronze Age Cities of the Third Millennium BC. Openarchive.icomos.org. 2013.
19. History of Science, Philosophy and Culture in Indian Civilization, 8(2). General Editor: D.P. Chattopadhyaya.  From Physiology and Chemistry to Biochemistry. Edited by D. P. Burma and Maharani Chakravorty. 2010.
20. R. P. Kulkarni. Layout and Construction of Citis According to Baudhayana, Manava and Apastamba Sulbasutras. 1987.
21. J. E. Schwartzberg. Introduction to South Asian Cartography, in ‘The History of Cartography’. University of Chicago Press. 1992.
22. S. N. Sen and A. K. Bag. The Sulbasutras of Baudhayana, Apastamba, Katyayana, and Manava. Indian National Science Academy. 1983.
23. Ramakrishna Bhattacharya. Origin of Geometry in India: A Study in the Sulbasutras. 2013.
24. Parameswaran Murthiyedath. Sulbasutras: Indian Texts on Sacred Geometry.  http://www.harekrsna.com. 2005.
25. Dharam Pal Kularia. Sulbasutras: A Critical Study. PhD Thesis, Maharshi Dayanand University, Rohtak. 2004.
26. Top 10 Civil Engineering Marvels.
27. Kapila Vatsyayan (editor). Concepts of Space: Ancient and Modern. Indira Gandhi National Centre for the Arts. 1991.

Acknowledgment: Thanks to Nripathi garu for his valuable feedback on terminology, and his ideas and comments that helped improve this post.