The Enduring Legacy of the Sulbasutras

Summary

Part 1: Why study the Sulbasutras — Objectives.

https://indicportal.orgsulba-sutras-the-indic-approach-to-engineering-1/

Part 2: Engineering Principles & Geometric Sciences — Harappan Period to Sulbasutras.

https://indicportal.orgsulbasutras-the-indic-approach-to-engineering-2/

Extended Abstract / Executive Summary

The Sulbasutras are the world’s earliest known text on geometrical sciences. Therefore, it is important to find out how the first results and rules of kshetraganita (geometrical science) came about. A brief review of this Ganita in the Sulbasutras that we undertake here provides useful information regarding:

Practical Applications

1. Can the ‘Indic mindset‘ and methods of the Sulbasutras be applied to solve contemporary problems?
2. Will the results be any better than that obtained using a modern/western approach?
3. We approach the first question through a study of the problem of arranging brick layers in Vedic fire altars (agni).
   • This problem yields a system of Sulba-Diophantine equations that are solved using combinatorial optimization ideas. We demonstrate the optimality of Baudhayana’s solution with respect to a specific brick-type selection objective.
   • This Vedanga contribution precedes the work of Sushruta, the Jaina text Bhagavati Sutra, and Pingala. Of course, the Sulbasutras themselves recall pre-existing ideas from Vedic tradition [1, 2].
   • We illustrate the engineering ideas that emerge from this problem using the example of the Ery (water tank) network of Tamil Nadu.
4. We contrast western and Indic optimization objectives to answer the second question in the affirmative.

Enduring Legacy

1. We use the ‘squaring the circle’ construction in the Sulbasutras to study the connection between its Kshetraganita (geometrical sciences) results and Vedic wisdom, and its contemporary lessons for professionals in all domains.
2. Indic scholars who have studied the Sulbasutras highlight the continuity of its Indic approach and terminology. Its methods have been consistently used and improved upon through the ages.
3. The pragmatism of Ganita (science of computation) and the practical excellence of Indic engineering do not arise from any separate materialism, but from dharma’s integral unity.

Engineering Optimization Applications

The study of ancient Indian texts cannot only be about restating remarkable facts about Bharata’s past achievements. In this section, we go further and identify useful applications and adaptations of Indic methods today in our own professional domain. We demonstrate Bharata’s continued practical relevance as a key source of solutions to real-life problems today. We have to do this without digesting [4] its ideas into a materialistic science that is divorced from India’s deep culture and dharmic traditions; otherwise it defeats the purpose and we end up becoming a part of the problem rather than the solution. We have to do this, as Dharampal recommended, as part of our overall effort to relocate ourselves to Bharatiya Chitta and Kala [11].

In this first section, we discuss one example of the sophisticated Kshetraganita concepts embedded within the construction of certain Vedic fire altars. This ganita can be adapted for meaningful innovation in engineering and analytical applications.

Author Note: the subject matter in this section is necessarily Ganita-heavy. We have moved much of the technical details to the appendix and kept the discussion at a high level in the main text to make it accessible to all readers.  Sulba terminology and results can be found in part-2.

Civil Engineering in the Sulbasutras

We start by summarizing briefly from a chapter of the excellent dissertation work of Dharam Pal Kularia [25] that discusses Civil Engineering aspects of Vedic altar construction:

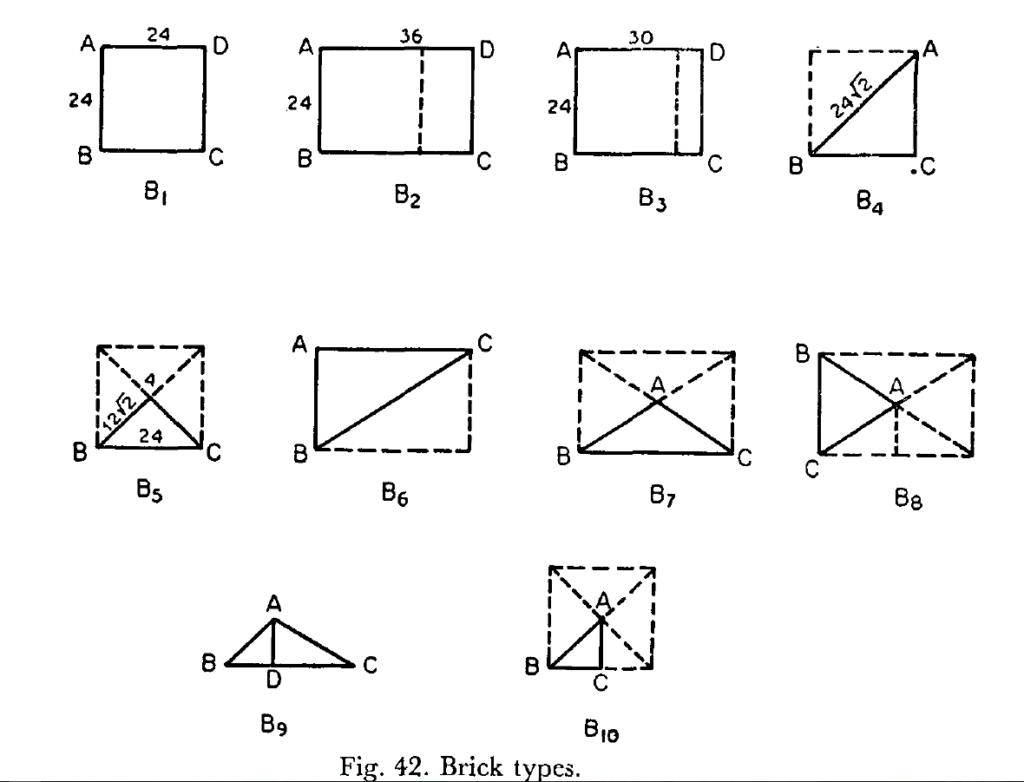
Different shapes and dimensions of bricks were employed in order to build Vedic fire altars of different shapes that represent various agnis. The patterns and dimensions of the bricks were variable and depended on the form of the fire altar being constructed.  Normal brick thickness was 6⅖ angulas, so that the height of five-layers would be 32 angulas. There were other brick types with a 5⅕ angula thickness.  Pancacoda and Naksat bricks were half the ordinary thickness [22]. Broken bricks were rejected and any reduction in brick dimensions due to heating was compensated by adding loose earth. Quality control ensured strength and consistency of building material. Some bricks were used only for measurement of area and not for the actual construction. At least seven different shapes of bricks of various length and width (and having the height stated above) have been observed:

1. Square (11 sizes: Chaturti, Panchami, Sasti, Dvadasika, Trayodasika, etc.). The sides of these various squares are conveniently represented in whole angulas that correspond to factors of 120 (1 purusa = 120 angula) and can be represented as simple fractions of a linear purusa. Interestingly, there are other square bricks mentioned whose lengths are not fixed but are vary depending on the altar size, i.e., length = f(altar area).
2. Rectangle (7 sizes: Ardhya-Chaturti, Ardhya Panchami, Brhati, etc.)
3. Triangle (19 sizes: Ardhya Chaturti, Paadestakaa chaturti, Ubhayi…)
4. Rhombus
5. Trapezium (5 sizes)
6. Parallelogram
7. Pentagon

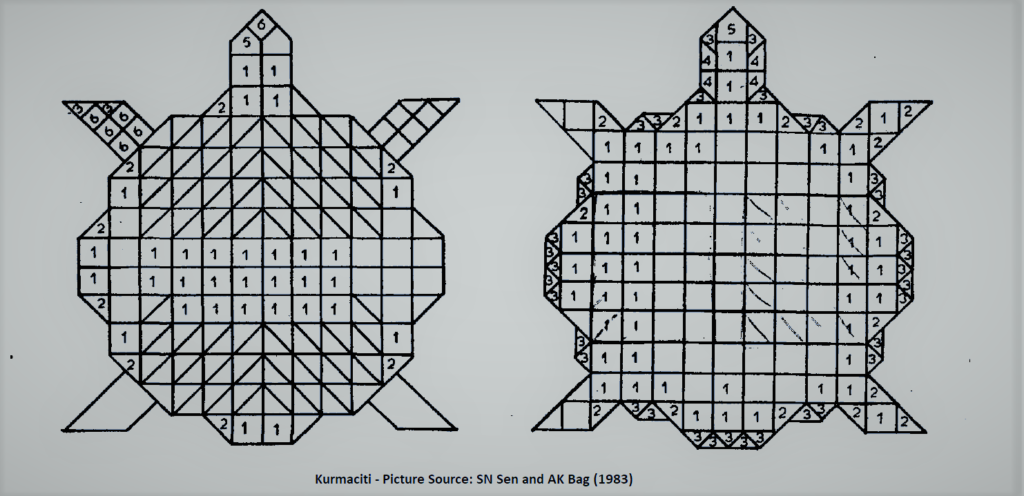
The Sulbasutras give a detailed description on the arrangements and types of bricks for several complex Kamyagnis. Two adjacent layers of a syenaciti (falcon shaped altar) are depicted side-by-side below, with color-coding. Note the symmetry within a layer and different patterns across layers.

An Altar Construction Problem in the Sulbasutras

Consider the simple case where only square bricks are used to complete the construction of the agni [1]. The altar builder has to decide a) which and b) how many of the available square brick types (design variables) should be selected.  Let us take a shot at identifying necessary and sufficient conditions to be satisfied by these design variables.

Necessary and Sufficient Conditions

The necessary conditions here represent brick selection decisions while sufficiency also includes brick placement decisions.

The necessary conditions must be satisfied to correctly establish the correspondences through the performance of Yagna:

1. Total number of layers in the citi = 5
2. Total area of a layer = A purusas (input parameter)
3. Total number of bricks per layer = B (input parameter)
4. Brick rifts of edge rows of adjacent layers cannot line up

These conditions can be translated into Ganita equations that must be satisfied by the values of the design variables. Requirements (1-3) are numerical, while (4) is a logical condition needed for stability: the inter-brick rifts cannot all line up one above the other to create a faultline across the citis (layers of the agni). A stable construction preserves the interconnectedness and unity across citis, and precisely reflects Vedic cosmology [5] and its description of consciousness [12].

Identifying sufficiency requires additional considerations including layout feasibility: the chosen parts should all be placed to fit together symmetrically and perfectly into the specified shape, leaving no area uncovered. Note that there is also a three-dimensional version where two different altars of different heights must have the same cubic content (part-2).

Where have we seen similar problems?

They are all around us! From laying out the different types of rooms in new hospitals, offices, and warehouses, to planograms that place quantities of selected products on retail store shelves, and in the tightly and safely packing a variety of cargo safely into aircraft, the list is limitless. Such problems are theoretically challenging to solve perfectly, but good solutions can be found for practical instances using Yukti that routinely save companies several million bottom-line dollars annually in operational cost.

Modern combinatorial optimization applications

• Vehicle routing (UPS/FedEx/Courier and postal services/trash pickup, etc.). Why do UPS trucks avoid left turns?
• VLSI design
• Minimum weight design of aerospace structures
• Scheduling (assigning a variety of specialist doctors, nurses, residents, medical attendants, etc.  to exactly cover the different duties in a hospital for the next week)
• Sequencing (air traffic control directing the landing order of arriving aircraft on a single runway, keeping in mind wave vortex effects)
• Evolutionary (‘genetic’) algorithms.

Inside an @amazon shipping crate… Any other Tetris-loving packing freaks out there that think this looks like heaven? pic.twitter.com/hQmbzZv1uF

— Kris Carlon (@kriscarlon) November 29, 2016

Sulba-Diophantine System of Equations

The necessary conditions when represented using Bijaganita (algebra) yield a system of indeterminate equations, which introduces uncertainty since such a system does not guarantee a unique solution. There are multiple combinations of brick sizes and shapes (in general) that can satisfy the necessary conditions. We call any such combination a feasible solution. One has to explore this diversity and find order within. In fact, homogeneity (unnatural order) in the chosen bricks produces an unstable construction, while complete heterogeneity (randomization) also produces undesirable solutions.

Unity in diversity: varied shapes and sizes in different combinations can unite to achieve the same desired correspondence between the microcosm and the macrocosm. The One manifests as the many.

Baudhayana identified a feasible solution for input values (A = 1, B = 21) that represent the  garhapatyagni, and for (A = 7½, B = 200) that arises in the construction of the syenaciti and other kamyagni [22].  Many scholars have studied this problem and generated a long list of feasible solutions.

These necessary conditions (1-3) are the earliest known instances of what was later termed ‘Diophantine Equations‘ by western mathematicians [26], where the unknown variables can only be integer valued. This is because we are not allowed to employ fractions of bricks. Consequently, a simple ‘greedy algorithm‘ is unlikely to work reliably. Sulba-Diophantine systems have a deep connection with combinatorics and computational complexity [32], and remain an area of active research.

Solving Sulba-Diophantine Equations

Bibhutibhushan Datta [1] identifies the following high-level Sulba approach:

1. Use reasoning to reduce the dimensionality of the problem to finding different solutions for the first two layers.
2. Find two different feasible combinations and assign to the first two layers.
3. The layer-1 brick placements are repeated for layers 3 and 5, while layer-2 is repeated for layer-4, and the necessary conditions are satisfied.
4. Note: another permutation is obtained by switching the solutions for the first two layers in (2) and then replicating (3).

Datta derived the solution obtained by Baudhayana for (A = 1, B = 21) using numerical and logical arguments. Our contribution here is to show that the necessary conditions are equivalent to solving a discrete (non-convex) optimization problem. The altar construction procedure in the Sulbasutras appears to be among the earliest applications of combinatorial optimization ideas.

A Combinatorial Optimization Formulation

"All models are wrong, but some are useful".
- George E. P. Box.
Models do not represent the Truth but some can provide guidance, delivering what they promise [31]. Nothing less, nothing more.

To solve this problem, we have to simultaneously select brick sizes and quantities for two adjacent layers. For this, we create two groups of discrete decision variables ‘Y’ (which brick types to select) and ‘X’ (how many of each type) and write the necessary conditions in terms of X and Y.  Suppose our objective is to identify a design having the fewest and preferably also the largest different brick types that satisfy the necessary conditions for two adjacent layers. A discrete decision optimization formulation can be written (see appendix-1) and solved using any standard mathematical optimization software package to obtain the best values of (X, Y) for any given input (A, B). 

For (A = 1, B = 21) we used this approach to re-obtain Baudhayana’s solution that chooses brick lengths (1/3, 1/4, 1/6). This result confirms that Baudhayana’s solution is not only feasible but also optimal with respect to the chosen minimization objective. 

Solution for (A = 1, B = 21)
12 bricks of length 1/4, total area = 0.75
9 bricks of length 1/6, total area = 0.25
total area for layer 0 = 1.0

5 bricks of length 1/3, total area = 0.556
16 bricks of length 1/6, total area = 0.444
total area for layer 1 = 1.0

We do not know for sure how Baudhayana obtained this particular combination, although Datta’s procedure is a plausible explanation. The fact that this solution is optimal for our minimization objective may provide some clues. To take this idea further, we solve another problem for which we also have Baudhayana’s solution.

For (A = 7.5, B = 200), we disallow the largest brick (1/3 Purusa) in keeping with the Sulba approach. We obtain a solution having the three largest brick types that are also obtained by Baudhayana who added a smaller brick type (1/10 purusa), perhaps to meet placement requirements. This (A, B) setting is typically used to construct complex shapes.

Solution for (A = 7.5, B = 200)
56 bricks of length 1/4, total area = 3.5
144 bricks of length 1/6, total area = 4.0
total area for layer 0 = 7.5

12 bricks of length 1/4, total area = 0.75
125 bricks of length 1/5, total area = 5.0
63 bricks of length 1/6, total area = 1.75
total area for layer 1 = 7.5

Apastamba and the commentators have stated several other feasible solutions including 5 and 10-brick type solutions. For shapes that have different angles, mechanically optimized solutions based solely on necessary conditions may not yield a satisfactory solution. This is an interesting area of research.

Here are some sample final solutions explained by the Sulba commentators for a particular syenaciti having bent wings [22]. Note that five brick types are used in the first layer, and ten in the second. The solution achieves symmetry, and we can see how the edge bricks differ between adjacent layers. Sen and Bag [22] also depict an underlying row and column grid in the arrangement, which would have been useful in brick placement.

The ten brick types used in this construction are shown below (dimensions in angulas). Note that B4 to B10 are triangular bricks. In many cases, we see that one or more smaller brick types combine to equal the area of a larger brick.

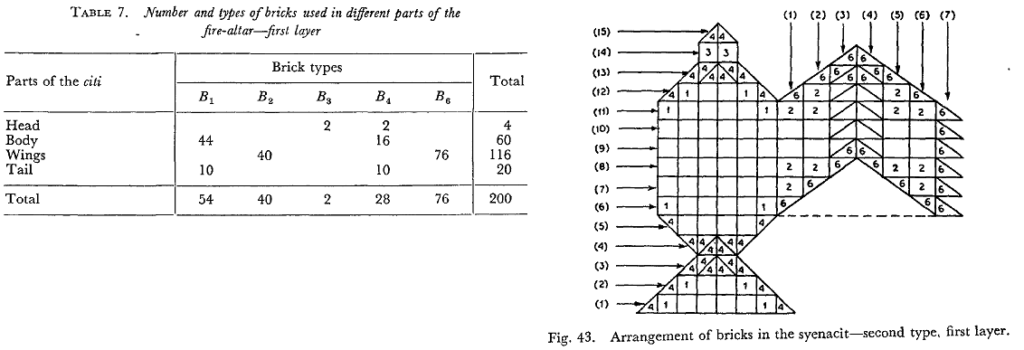
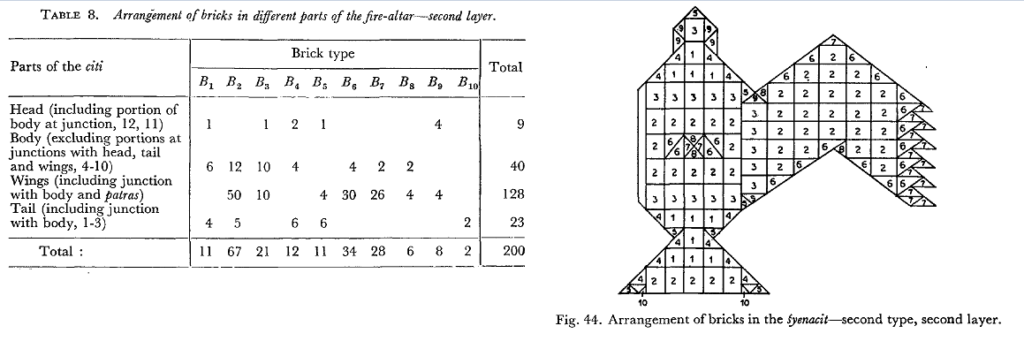
It is clear that the Sulba authors were comfortable working with different brick shapes and quantities to generate not just different combinations but producing multiple feasible combinations, which is more challenging. This work predates the contributions of Sushruta and Pingala to combinatorics [33].

Permutations and Combinations

Solutions to a Sulba-Diophantine system are easy to verify but difficult to find. Given a tentative solution, it is easy to confirm if it is feasible. We only allowed square bricks in the combinatorial optimization formulation. If we permit rectangles and triangles of various sizes, then the theoretical number of different feasible combinations would increase drastically. If this is not enough, the potential number of permutations in which the bricks of any one of these solutions can be placed to form the shape of the citi is also huge. A brief note on the altar construction problem’s computational complexity is given in appendix-2.

It is to the credit of the Sulbakaras that they empirically identified feasible permutations and combinations practically required for performing Yagnas, without getting lost in the maze of worst-case theoretical complexities like some computing theorists today.

Combinatorial problems have been studied in India (at least) since the time of the Sulbasutras. Sushruta Samhita enumerates all (2n − 1) combinations arising from n = 6 different tastes. The Jaina Bhagvati Sutras discuss permutations and combinations. Pingala's contributions in Chandahsastra are monumental. Brhat Samhita of Varahamihira generates combinations of perfumes [33]. 

Srinivasa Ramanujan was solving such practically useful but difficult combinatorial decision optimization problems as a high-school kid in Kumbakonam.

Exchange-moves in the Sulbasutras based on commentary

In the commentary on the Sulbasutras [22], we find explanations of exchange-moves during the placement of bricks that reduce the infeasibility of a current solution. This is non-trivial since not all exchanges are valid. A valid series of moves should preserve symmetry, stability, and eventually fill up all the open spaces exactly (see appendix-3 for more notes).

Former US President Barack Obama's speeches during crises sometimes used the phrase "it will get worse before it gets better". 

Tamil saying: "catch a big fish by giving up smaller fish as bait" :)

This is how Sulbasutra-moves end up with a better solution.

Suppose a citi is short of its target brick count by a few bricks, the Sulba method does not always simply try to add bricks; sometimes it will backtrack and remove bricks to obtain a temporarily worse solution, then search and add a better combination of bricks that results in an improved state compared to the initial state. We provide some examples below [22]:

• Ubhayata Prauga (rhombus): 10 B1 (ten bricks of type B1) are removed and replaced by 20 B2 to achieve feasibility in terms of number of bricks and leaving the covered area unchanged.
• Syenaciti: In each of the 3rd and 4th row from the south, 4 B1 are removed and replaced by a combination of 6 B2 and 1 B3.
• Dronacit (square trough):  This is a sequence of multi-exchanges. The number of B1 is first increased by 4 and then decreased by 12.
  • 4 B2 replaced by 4 B1
  • 4 B3 and 12 B1 together removed and replaced by 24 B3

A simple and general improvement rule is discernible from the analysis of the commentary of Dvarakanatha [22] and is presented in appendix-3.

Some Engineering Ideas

To a skilled practitioner, the chaos due to the indeterminate nature of such problems becomes the very source of practical innovation, flexibility, and improvement.

1. Redundancy in design
   •  If some brick types are unavailable or damaged, they can be substituted by alternative brick types to recover feasibility. The Sulbasutras, like other Hindu texts, do not enforce unnecessary restrictions.
   • Building sufficient redundancy improves reliability in an uncertain world, resulting in a sustainable system. We can see in this the ‘self-organizing’ principle of dharma at work. The Vedic chant is an application of this (upcoming post).
2. Overcoming local optima to achieve optimality
   • Multi-exchange moves help overcome local optima where a solution is ‘stuck’; solution quality worsens if you try exchanging any single component.
   • Sulbasutras’ exchange moves are a kshetraganita version of a ‘local neighborhood search‘ in computer science.  At a high-level, the idea resembles the Lin-Kernighan Heuristic [27], a key subroutine within sophisticated combinatorial optimization software.

Anybody who studies the sacred Sulbasutras seriously is likely to walk away with ideas that will be useful in their own domain.

Have such ideas been used in India?

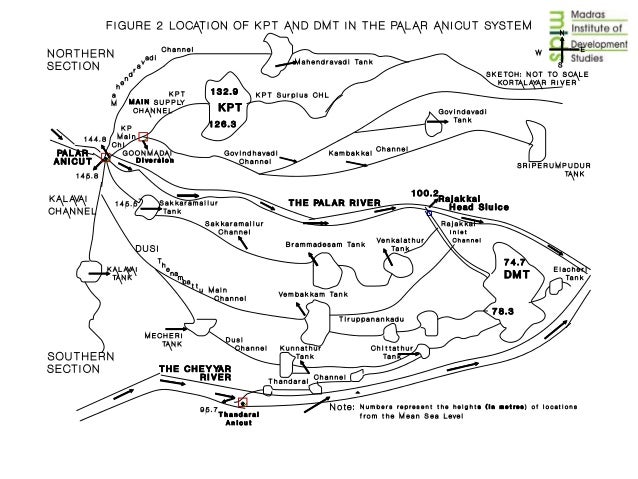
The interconnected Erys were the decentralized water reservoir systems of Tamil Nadu. It is a remarkable feat of Indic engineering that ingeniously combines the two Indic ideas of unity through self-organization, and optimization in harmony with Rta. Dr. JJ Bajaj remarks on the Ery network [29]: “together they formed a closely knit whole so that the outflow from the one at a higher level supplied the one at a lower level, and so on. This chain of tanks was so complete and inter related within itself that the British engineers of the nineteenth century felt that it would have been impossible to add another tank to the chain.”

The Yukti of indigenous engineering produced an optimal design that worked beautifully in practice: a self-contained, sustainable, decentralized solution that was maintained locally, and serving local needs.

Difference between Indic & Modern/Science Objectives

There is a fundamental difference between modern innovations and the Indic approach enshrined in the Sulbasutras. In part-2, we contrasted Vijnana-Ganita with modern science-mathematics, which is related to the discussion here.  These modern applications are indeed amazing but pursue purely material objectives such as improving one’s own system’s efficiency or reducing one’s own operational costs, while adopting a contractual/legalistic view of the harm caused by such decisions to anything that falls ‘outside’ the boundaries of their own system.

Such an approach can become cynically exploitative of the environment; and even when it does address environmental concerns, it is for the benefit of their human population and not for the environment itself, as explained in the video discussion below.

In contrast, the Indic objective reflected in the altar constructions of the Sulbasutras is to reestablish harmony with Rta. Material benefits are obtained here too by making better decisions, but as a derivative of serving this transcendental goal. Such a dharmic mindset actively minimizes the negative impact of decisions on the environment and himsa to those outside the system so that ultimately there is no ‘outside’.

There is mutual respect between those 'inside' and 'outside' the system that makes this possible. Compare this with the western idea of mere tolerance of 'outsiders'. How are these attitudes shaped? Plants and animals (and women, until recently) have no soul, but all have atma [4].

The sublime Shanti Paatam at the start of the Purusha Suktam of the Rig Veda encapsulates this universal objective through an invocation to the divine at the start of a Yagna [30]. It seeks the well-being of all the plants, creepers, birds, animals, and peace and tranquility for all mankind.

Such an enlightened and integral vision is sustainable and necessary for dharmic development. The traditional Indic objective is adhered to even it means a reduction in material benefits to self. A decision that the myopic materialist views as an unnecessary loss, an Indian who believes in karma and rebirth can see as Punyam accrued, whose value is transcendental and persists beyond this lifetime. It represents a practical, decentralized, self-organized decision optimization. This is a traditional Indian way of life rooted in Dharma. We will dive deeper into this in an upcoming post.

Ganitananda: Attaining the Infinite in the Finite

"the Sanyasi realized that the great is to be found in the small, the infinite within the bounds of form, and the eternal freedom of the soul in love". 

"...this has been the subject on which all my writings have dwelt -the joy of attaining the infinite in the finite".
- Gurudev Rabindranath Tagore in 'Nature's Revenge'.

It is no accident that the Ganita approach in the Vedangas to represent the infinite in the finite mirrors our own path to self-realization and uncovering the divinity within ourselves. Ganita’s Vedic roots are unmistakable in its texts, over the ages. In the Vedanga Jyotisha (Yajusha recension [28]), the verse:

Vedaa hi yagnyaartham abhipravrittaah

is translated by Prof. T. S. Kuppanna Sastry: ‘the Vedas have indeed been revealed for the sake of performance of Yagna‘. The amazing results in the Sulbasutras and Jyotisha emerge from the Bandhus established for the duration of the Yagna. Datta [1] recognizes this source via a critical observation: “geometrical methods for the solutions to measurement problems were known very early, for without knowledge of the underlying geometry, these precise correspondences required for yagnas cannot be established.” Dr. Saraswati Amma [2] reiterates this primary objective of the Sulbasutras: “self-realization and resulting deliverance from birth and death were the most legitimate purpose of life, and those sciences which were supposed to further this purpose directly or indirectly were most assiduously pursued“.

Ganita's dharmic roots are the reason for its 'unreasonable' practical effectiveness, sustainability, and universality. Indian discoveries in multiple fields traveled to Europe and were indispensable for the development of modern applied mathematics, engineering, and science in the west.

Such a ganita is not only universally applicable; over time it becomes a natural way of thinking and problem solving. As a case-study, we examine a Sulba construction  that yields an inexact result to complement Baudhayana’s famous exact SQD result.

Circling the square obtained by squaring a circle

The Sulbasutras state the steps to construct a square whose area is approximately equal to that of a given circle, and to circle a given square. In part-2, we reported the achieved accuracy of this transformation to be more than 98%. Prof. John Price, in his study of the Sulbas [12] analyzed the internal consistency of the calculations in the Sulbas. Starting with a circle of any diameter ‘d₁‘, we can cycle through the steps in Baudhayana’s rules to square the circle and re-obtain a circle of diameter ‘d₂‘ from this square (see appendix-4). The resultant percentage error between d₁and d₂ is:

Consistency error ~ 0.00024% (less than 3 in a million)

The internal consistency (transforming the transformation) is nearly 100%. This suggests that Baudhayana’s numerical method for squaring the circle was obtained by inverting the square-to-circle result. For any ‘in-the-trenches’ engineer who is actually building stuff that works, a couple of features regarding this result stand out.

• 1. The solution isn’t perfect, but is perfectly good. 

The first observation highlights the need to work with the ‘chaos’ found within the order in nature.

A) This result exhibits a self-correcting property of the transformations prescribed by Baudhayana. The ~2% error in each step does not add up but almost completely cancels out [12]. This leads to several learning points and we cite just a few:

• This result represents a simple form of mathematical duality.
• A great lesson for those who will be building systems having many moving parts. The whole should be stronger than its individual, diverse parts, not weaker.
• It motivates the idea of ‘risk-pooling’ to achieve a reduction in overall uncertainty, which is critical to designing robust supply chains (for example). It was also used to set up India’s national health insurance scheme a few weeks ago.

B) The tension-free preference for a perfectly practical solution over the quest for infallible perfection reflects the innate Indian poise in the face of uncertainty. Its Vedic origin is explained in the words of Rajiv Malhotra [4] using the metaphor of the Samudra Manthana that “points the way to the transcendence of both order and chaos, which are brought into delicate equilibrium and ultimately subordinated to spiritual realization. The story of the Samudra-manthana is not intended to be taken literally. Indeed, the ultimate uncertainty of knowing how the universe came about is given eloquent expression in the famous ‘Hymn of Creation‘ in the Rig Veda (X.129)“.

The fire altar that is precisely constructed and specified down to the smallest detail also incorporates uncertainty explicitly, grounding the manifest in the unmanifest [4]. Nature reveals order while retaining an indelible element of mystery. From a Kshetraganita perspective, this attitude eliminates the anxiety with measuring and calculating the area enclosed by curved figures, which can never be exact but can be accurate enough for a given application. We see this attitude in the dvikarani (√2) calculation as well. The solution can always be improved and the degree of uncertainty reduced through Yukti. Sulba Vijnana harmoniously integrates several opposites such as inexactness-exactness in measurement, imprecision-precision in altar construction, and uncertainty-surety in results and rules.

C) This pragmatic attitude is crucial to problem solving in engineering practice. It reduces the chances of getting carried away by theoretically perfect but practically unviable mathematical models. It encourages practitioners to build high-quality and robust products that take into account their fallibility when subject to the vagaries of nature.

"My name is Ozymandias, King of Kings";
Look on my Works, ye Mighty, and despair!
Nothing beside remains. Round the decay
Of that Colossal Wreck, boundless and bare,
The lone and level sands stretch far away.
- Percy Bysshe Shelley.

For example, intensity of earthquakes, forest fires, and flooding remain quite unpredictable. These numbers follow a ‘power law’ and their mean value doesn’t usefully represent the overall distribution. Consequently, structural engineers develop earthquake resistant (not proof) skyscraper designs, and hydro engineers build systems to withstand 100-year floods, based on an explicit admission of fallibility. After all, there are only three things certain in this world – death, taxes, and rebirth. As engineers, we have the right to do our best, but the phala isn’t in our hands.

Unlike the ‘seven wonders’ of the ancient world outside Bharata, Indic engineering and architecture have both an outer and inner layer of genius. We have to scratch below their surface to experience the ultimate wonder of realizing the infinite in the finite.

• 2: The achieved accuracy of the construction holds for all squares or circles.

The second observation reveals the order that emerges from within the apparent chaos of nature.

Using only a finite number of construction steps, the Sulbasutras yields a result whose percentage accuracy and internal consistency is valid not just for the specific nityagni construction but holds for all future square-circle transformations of any size. This result is scale invariant and universally applicable. It isn’t one of those abstract theoretical bounds but is demonstrable in real life applications.

Panini’s Ashtadhyayi and Bharata’s Natyasastra (ganita in Natyasastra) are among the divine examples of the finite attaining the infinite that transformed the world. Simpler applications of the principle of the One manifesting as the many and the apparent differentiations being just the different forms of the One [4] can be seen all over India. The graceful Saree worn by hundreds of millions of women from ancient times to this day is a continual reminder of this principle that hides in plain (or spectacular) sight. In Sulba Vijnana itself, the contextually flexible and versatile Rajju replaced the rigid Bamboo rod (Venu) as a preferred means of measurement [1].

Epistemological Continuity

The western mathematical quest to conquer the infinite is sharply different from the Indic (Vedic) approach. The ‘Indian rule generation versus abstract theorem’ approach is discussed in our introduction to Ganita [29], while part-2 compares Indian self-verifying computing with the self-evident axiom based approach [31]. The microcosm mirroring the macrocosm for a limited duration of the Yagna. The Ganita approach too generates tentative results that are to be improved over time. Datta [1] summarizes the ancient Hindu approach of stating theories that are in turn, refuted by newer theories, etc., which is a hallmark of scientific progress achieved and a systematic approach at work in ancient India.

Datta clarifies that what he states as postulates of the Sulbas are not in the Euclidean sense but are results that can be validated in real life since every one of these postulates are empirically demonstrated. After the description of the geometrical construction for a proposition, the Sulbakaras often remarked ‘sa samaadhih‘, i.e., this is the construction. This is archetypal of the Indic approach to generating new results and Datta found a similar remark in the work of Bhaskara-2 more than a thousand years later, again highlighting its continuity. Many ideas in the Sulba Sutras were pre-existing in Vedic works, including the Satapatha Brahmana and Taittriya Samhita dating back to the 3rd millennium and earlier [1]. Sulbasutra terminology too has persisted through Ganita works in later times [2].

It is worth restating that in the contributions of Harappans, from Baudhayana and Lagadha to Aryabhata, from Madhavan Emprantiri to Srinivasa Ramanujan, one can uncover the continuity in the approach to generating new results. India’s amazing epistemological continuity thwarts western Indology’s optimistic speculations about foreign methods entering ancient India, and claims of Indic results being enunciated earlier elsewhere. The dates assigned to some of these Ganita contributions are getting pushed further back as more discoveries about ancient India come to light. From the many examples of Harappan engineering (4th-3rd millennium BCE), the earliest Vedic works, and the Sulbasutras, it is apparent that the Hindus possessed and employed their own unique approach to independently generate, apply and validate new results in the real world to the satisfaction of their peers.

Saraswati Amma’s crucial observation [2] puts this discussion in perspective: Jagannatha in the court of king Jayasimha in the 18th century CE was the first to translate Euclid’s elements into Sanskrit, and even then, perhaps inspired by the Arabs.

Conclusion

The fragmented and materialist approach adopted by modern engineering and science is producing an increasingly skewed progress that is unsustainable. The problem of religious dogma versus science that is plaguing the western discourse to this day is alien to dharma traditions [4]. Such a reductive approach and limited objective is incompatible with dharma traditions. 

Dharmic India recognizes no separation of all reality, whether phenomenal or non-phenomenal, from the divine [4]. This integral unity of dharma and Ganita’s remarkable pragmatism are not mutually exclusive. Pragmatism should not be confused with materialism. Our research into the Sulbasutras suggests the exact opposite to be true: Hinduism’s Integral Unity is the very source and motivation for the powerful results of Ganita and the harmonious excellence achieved by Indic Engineering.

---

References

1. Bibhutibhushan Datta (Swami Vidyaranya). The Science Of The Sulba: A Study In Early Hindu Geometry. University of Calcutta. 1932.
2. Saraswati Amma. Geometry in Ancient and Medieval India. Motilal Banarsidass Publishers. 1979.
3. Kapila Vatsyayan. The Square and the Circle of the Indian Arts. Abhinav Publications. 1997.
4. Rajiv Malhotra. Being Different: An Indian Challenge to Western Universalism. Harper Collins. 2011.
5. Subhash Kak. The Astronomical Code of the Ṛgveda (Third Edition). 2011.
6. Rajiv Malhotra. Indra’s Net: Defending Hinduism’s Philosophical Unity. Harper Collins. 2014.
7. Kosla Vepa. The Origins of Astronomy, The Calendar, and Time (Second Edition). 2010.
8. Prakruti Prativadi. Rasas in Bharatanatyam: First in a Series on Indian Aesthetics and Bharatanatyam. Creative Space. 2017.
9. N.R.I Pathi. Dharmic Development. Andhra Cultural Portal. 2014.
10. Prakruti Prativadi. The Bharatanāṭyaṃ Yajña. Swadeshi Indology-3 Information Handout. 2017.
11. Dharampal. Collected Writings in 5 Volumes. Other India Press. 2000.
12. John Price. Applied Geometry of the Sulba Sutras. Department of Mathematics, Maharishi University of Management, Iowa. 2000.
13. Amartya Kumar Dutta. Was There Sophisticated Mathematics During Vedic Age? in ‘An anthology of disparate thoughts at a popular level‘. ISIREA, Kolkata, 2016.
14. K. Ramasubramanian. The Origin and Growth of Mathematics in India. R C Gupta Award Lecture, IIT Bombay. 2010.
15. Michel Danino. Lost River: On The Trail of the Sarasvati.  Penguin Books. 2010.
16. Michel Danino. New Insights into Harappan Town-Planning, Proportions and Units, with Special Reference to Dholavira. Man and Environment (33). 2008.
17. Rima Hooja. Channeling Nature: Hydraulics, Traditional Knowledge Systems, And Water Resource Management in India – A Historical Perspective.
18. Michael Jansen. Mohenjo-Daro, Indus Valley Civilization: Water Supply and Water Use in One of the Largest Bronze Age Cities of the Third Millennium BC. Openarchive.icomos.org. 2013.
19. History of Science, Philosophy and Culture in Indian Civilization, 8(2). General Editor: D.P. Chattopadhyaya.  From Physiology and Chemistry to Biochemistry. Edited by D. P. Burma and Maharani Chakravorty. 2010.
20. R. P. Kulkarni. Layout and Construction of Citis According to Baudhayana, Manava and Apastamba Sulbasutras. 1987.
21. J. E. Schwartzberg. Introduction to South Asian Cartography, in ‘The History of Cartography’. University of Chicago Press. 1992.
22. S. N. Sen and A. K. Bag. The Sulbasutras of Baudhayana, Apastamba, Katyayana, and Manava. Indian National Science Academy. 1983.
23. Ramakrishna Bhattacharya. Origin of Geometry in India: A Study in the Sulbasutras. 2013.
24. Parameswaran Murthiyedath. Sulbasutras: Indian Texts on Sacred Geometry.  http://www.harekrsna.com. 2005.
25. Dharam Pal Kularia. Sulbasutras: A Critical Study. PhD Thesis, Maharshi Dayanand University, Rohtak. 2004.
26. Bibhutibhushan Datta. The Origin of Hindu Indeterminate Analysis. Archeion (13). 1931.
27. David L. Applegate, Robert E. Bixby, Vasek Chvatal, William J. Cook. The Traveling Salesman Problem: A Computational Study. Princeton University Press. 2006.
28. KV Sarma and Kuppanna Sastry. Vedanga Jyotisa of Lagadha In its Rk and Yajus Recensions. With the Translation and Notes of Prof. T. S. Kuppanna Sastry. Critically edited by K. V. Sarma. Indian National Science Academy. 1985
29. J. J. Bajaj. The Indian Tradition in Science and Technology: An Overview. PPST Bulletin. www.samanvaya.com.
30. Oppiliappan Koil V Sadagopan. Purusha Suktam: Annotated Commentary in English.
31. Roddam Narasimha. Some thoughts on the Indian half of Needham question:
    Axioms, models and algorithms. 2002.
32. Michael R. Garey, and‎ David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. 1979.
33. N. L. Biggs. The Roots of Combinatorics. Historia Mathematics 6 (1979), 109-136.

Acknowledgment: I cannot thank Nripathi garu enough for his support, patience, and critical feedback that shaped this series on the sacred Sulbasutras.

Postscript:  Foreign math approaches may have visited India, but if they did, they were largely ignored (or guests at best), and did not establish a solid foothold until the 18th century CE as discussed in the section on continuity.

 *Why?* Here is one argument:
 1. To be valid knowledge, any new claim has to be compatible with dharma
 thought systems and their established standards of acceptance.
 2. European mathematics based on deductive (Aristotelian) logic was
 inadequate in this regard (see ICP post on Ganita).
 3. Vedic approach is integral:
 → employs computation|construction-as-verification (see part-2)
 → hence results *had to be independently generated* using this Indic approach, thereby also verifying its correctness and compatibility with dharma.

Appendix-1: Discrete Optimization Formulation

Suppose we are given the following data:

List of 8 square bricks of side length 1/L(i) of a purusa, where the allowable values of inverse-length L = {3, 4, 5, 6, 8, 10, 12, 15}, where

Brick-type index i = 0, 1, .., 7. We can use this to index inverse brick lengths as L(0) = 3, L(1) = 4, etc, and L(i) in general.

Layer index j = 0, 1 that index the two layers that have to be simultaneously solved.

There are two decision variables whose values have to be identified:

Y(i), a Boolean (binary) variable that is 1 if bricks of length 1/L(i) purusa is selected, and 0 otherwise.

X(i, j), a non-negative integer-valued variable representing the number of bricks of length 1/L(i) purusa in layer j.

Combinatorial Optimization Formulation for Square Bricks

# brick selection optimization objective
Minimize sum(i) L(i)*Y(i)

# establishing the correspondence principles
sum(i) X(i,j)/L(i)² = A; for j = 0, 1.
sum(i) X(i,j) = B; for j = 0, 1.

# logical conditions between the design variables
B*Y(i) ≥ X(i,j) ≥ 0; for all (i, j).
sum(j) X(i,j) ≥ Y(i) for all j.

# anti-symmetry stability restriction
sum(i) L(i)*X(i,0) ≥ sum(i) L(i)*X(i,1) + 1

Y binary, X integer.

This formulation can be generalized to any brick shape:
For square bricks, area in purusa S(i) = 1/L(i)²
For rectangular bricks (L, W), area in purusa S(i) = 1/{L(i)*W(i)}

Appendix-2: Computational Complexity

Note that the number of available brick shapes and dimensions are finite. Therefore, the total population of different combinations is also finite but rapidly increases ("exponential growth") as the altar parameters and available brick choices increase. Brute-force enumeration of all possibilities to find a best answer is impractical. 

There are two themes in contemporary combinatorial optimization: a) proving optimality. This is largely theoretical, but can be of practical value sometimes. b) finding improved solutions. The focus of this post is on this latter practical aspect.

The general Sulbasutra altar construction problem appears to be 'NP-Hard' (its decision counterpart is NP-Complete) [32]. It is unlikely that efficient algorithms exist for this problem class (unless P = NP). This theoretical limitation does not however mean that good solutions to such combinatorial problems cannot be found in practice.

Appendix-3: Improvement Rule

a) any sequence of moves should be area conserving

b) when there is a deficit of brick count: remove multiple larger bricks and replace with a larger number of one or more smaller sizes

c) when there is a surplus of brick count: remove many smaller bricks and replace with fewer large bricks.

For example:

1.  given a target deficit of 2n bricks to be made good, first remove 2n bricks of area S.
   • This temporarily worsens the solution, increasing the deficit to 4n and the uncovered area by 2nS.
2. Find 4n bricks among the available (smaller) sizes such that the sum of their areas = 2nS and satisfies placement requirements.
   • This is equivalent to solving the original problem but with smaller inputs (A = 2nS, B = 4n), i.e., it generates a partial solution.
3. As a simple example, we can select 4n bricks each of area S/2. The final deficit is zero, and the net change in covered area after the moves is also zero.
4. Repeat this heuristic until feasibility is achieved (hopefully).

Appendix-4: Internal Consistency

if we square a circle of diameter d, the side of the square (2a) is given by:
2a = (9785/11136)*d —(Equation 1)

If we circle a square of side 2a, the resultant diameter d is given by:

d = 2a[1+(√2-1)/3]—(Equation 2)

Eliminating ‘a’ from equations 1 and 2, and using the Sulba value for √2

d ~ d*(9785/11136)*(1607521/1412496)

1 ~ 15729592985/15729555456 ~1.0000023858907

percentage error ~ 0.000239%