This introductory blog provides the background for an upcoming Ganita series here at ICP. All emphasis within quotes is by this author.

Losing one glove is certainly painful,

but nothing compared to the pain,

of losing one, throwing away the other,

and finding the first one again. 

—Piet Hein, Danish Mathematician

Introduction

Though often compared with the field of Mathematics, Ganita is best defined as the science and art of computation that originated in India. This is based on the definition offered by Ganesha Daivajna in his commentary (1540CE) on the classic Ganita treatise Lilavati of Bhaskara-2 [1]. Other descriptions of Ganita include ‘computing science’, ‘reckoning’, ‘science of counting’, ‘science of calculation’, etc. Although Ganita is related to Mathematics, they are not the same. The practice of Ganita cuts across multiple areas including Mathematics, Computing, Science, Logic, Analytics, etc. The term ‘Mathematical Sciences‘ may be closer to Ganita.  There is no exact English equivalent for the Sanskrit word Ganita, and it is better to use ‘Ganita’ as is.  

An ancient extant work of Ganita is the Sulvasutras (Sulbasutras), which are the oldest texts of geometry dating back to 800 BCE or earlier [1]. A verse in the Vedanga Jyotisha (1100 BCE or earlier) attests to the pride of place occupied by Ganita in ancient India.

Like the crest on the peacock’s head,
Like the gem in the cobra’s hood,
So stands Ganita*,
At the head of all the sciences.

The Ganita Culture of India

Indians are famous for their Ganita prowess. The greatest Persian scholar of his time, Ibn Sina (aka Avicenna, 10-11th CE) found that an Indian vegetable vendor’s calculating skills were superior to anything he knew [1].  European visitors during colonial times were astounded and remarked that “the natives of India are remarkable for the facility with which they acquire the mathematics; and indeed they excel in anything in which figures or numbers are concerned”.  The East India Company promised a reward of twenty pounds to its soldiers if they could learn arithmetic from the Indians [2]. It is well known that the word ‘algorithm’ comes from Algorismus, the latinization of ‘Al-Khwarizmi’, the person who translated several Sanskrit texts of Ganita (e.g. those of Brahmagupta) into Arabic. Thus, an algorithm implies the Indian method of computation, i.e., ‘Ganita’.  Much of Ganita and its methods made its way to Europe, first through Arab translators, and later through Jesuit priests stationed in India [3].

The Ganita curriculum in Indian schools prior to European colonization was functional, pragmatic, autonomous, and also guided by, and customized to local needs. The method of teaching Ganita in schools was ahead of its time. Researchers attribute this success to: “a culture of pedagogy grounded in a form of memory very different from the modern associations of memory with rote or mechanical mode. This could be characterized as recollective memory where memory practices constituted a distinct mode of learning and not merely aids to learning”[2]. 

To this day, the Ganita prowess, ability to recall, and the computing literacy of Indians is second to none. It is no coincidence that Indians excel in STEM disciplines. Understanding how Ganita works and what lies at its core is useful and interesting. Ganita can be a refreshing complement to the dull and dry Math taught in schools today. Training young minds to apply the Ganita approach to problem solving can offer them a competitive advantage. Manjul Bhargava, Fields Medal winner, is an example of a contemporary scholar who scaled the peak of Mathematics and is also well versed in Ganita and aware of its Indian tradition.

Above all, Ganita is a precious part of India’s heritage and culture. It is inevitable that India will regain its lost political and economic freedom. But this can and must be achieved without selling out or forgetting its traditions and indigenous knowledge systems like Ganita, Yoga, and Ayurveda. The trauma of a civilization that realizes that it squandered away its priceless cultural treasures will be unbearable.

The Scope of Ganita

This introductory video of an excellent IIT lecture series on Indian contributions to mathematics provides a good overview of Ganita. It was recognized that Ganita’s applications span the secular and sacred domains without any artificial distinction between the two. This integral nature of Ganita was embraced by all the great Buddhist, Jaina, and Hindu scientists and astronomers since ancient times.

India’s Rishis and Ganita experts attributed their astonishing insights to a sacred source. The practice of Ganita offered a valid means of attaining this infinite, transcendental knowledge, and through this process, skilled practitioners also came up with ingenious practical solutions to a variety of problems.

Sacred Source of Ganita

Panini (BCE)

The Siva Sutras in Panini’s Ashtadhyayi, which one can consider as an early example of the Indian approach to science, were revealed to Panini (pronounced: Paanini) via the sacred sounds from Shiva’s Damru. In fact, some scholars consider the Indian approach to math and science to be the ‘Paninian approach’ [1]. Indian kids traditionally start their exam papers with a small notation above the top of the page as an invocation to Ganesha (e.g. Tamil kids draw a tiny ‘Pillayaar Chuzhi’). This is an ancient practice of a tradition that reveres wisdom and learning, and one that is worth preserving. From Panini to Ramanujan, we see a great line of Ganita scholars beginning their works with an explicit tribute to a divine deity and their sacred cosmology.

Aryabhata (499 CE)

In his Aryabhatiya, the great astronomer Aryabhata who’s statue today adorns UNESCO, begins by paying obeisance to Brahma who is recognized as “the god who is the one and the many” [5]. This is a pertinent point from a Ganita perspective which we shall see later. We learn the following from the commentaries on Aryabhatiya:

• Bhaskara I : “It is said : ‘(Aryabhata) who exactly followed into the footsteps of (Vyasa) the son of Parasara, the ornament among men, who, by virtue of penance, acquired the knowledge of the subjects beyond the reach of the senses and the poetic eye capable of doing good to others’.” 
• “Aryabhata’s devotion to Brahma was indeed of a high order. For, in his view, the end of learning was the attainment of the Supreme Brahman and this could be easily achieved by the study of astronomy”.
• Aryabhata is obtaining new results by navigating through an existing ocean of knowledge: “Having taken a deep plunge into the entire ocean of the Aryabhata-sastra with the boat of intellect, I have acquired this jewel, the Karana-ratna, adorned by the rays of all the planets.“

Nilakantha Somayaji (1444-1544 CE)

He was a great Ganita expert and astronomer from the Kerala School (who can be viewed as Aryabhata’s intellectual successors). Nilakantha was also recognized for his mastery of all six darshanas of Hinduism [6]. His great work Tantrasamgraha begins with an invocation to Vishnu. Commentators on this work note that the invocations recognize Vishnu as both the material and the efficient cause of the universe [7].

Srinivasa Ramanujan (1877 – 1920)

Ramanujan attributed his amazing results to Goddess Namagiri. His statements reveal a firm belief and appreciation of Hinduism and its understanding of ultimate reality. The source of his knowledge was beyond anything cognizable by ordinary senses. Thanks to his biography [8], there’s a lot of material describing, from a western perspective, Ramanujan’s amazing ability, and the following samples provide clues about his methods. Ramanujan is a role model for aspiring young Indian mathematicians and scientists, and this was acknowledged by the Nobel Laureate Astrophysicist, S. Chandrashekar.

• “Ramanujan’s belief in hidden forces and the powers of the supernatural
  was never, at least back in India, something about which he felt the need
  to apologize or keep quiet“
• Ramanujan “had grown up on the Indian gods and the relaxed fluidity of Hindu belief. In him, the natural and the supernatural, Jacobi and Namagiri, Number
  and God, found a common home, stood in something like an easy intimacy.“
• “…the mystical streak in him sat side by side, apparently at perfect ease, with raw mathematical ability may testify to a peculiar flexibility of mind, a special receptivity to loose conceptual linkages and tenuous associations.“
• “his openness to supernatural influences hinted at a mind endowed with slippery, flexible, and elastic notions of cause and effect that left him receptive to what those equipped with more purely logical gifts could not see; that found union in what
  others saw as unrelated; that embraced before prematurely dismissing“

Each of these independent Indian thinkers freely moves between the transactional and the sacred domains without anxiety. Their work was firmly anchored in Dharma, and serving this integrated unity. The deities invoked include the celestial Hindu trinity and the Devi. Dharma is not the same as religion [10], and this is not theology or missionary zeal working overtime to fudge mathematical models in order to make it compatible with religious scripture, prophecy, and God. Rather, Ganita’s findings arise from a seeker’s quest to learn the truth about the nature of ultimate reality. The Bhagavad Gita (verses 9.4, 3.40-41) recognizes the empirical to be rooted as well as culminating in the transcendental [13]. Ganita is a sacred and valid path to reach the transcendent, and the continuity in the views of four great scholars from different time periods in Indian history drives home this point. Given the importance attached to this sacred source by its foremost practitioners, it is more accurate to view Ganita as the integral science of computing.  Attempts to equate Ganita to a purely pragmatic and secular science or math is inaccurate and reductionist.

The creation stories in the Vedas lend themselves to a rich interpretation that trace out a fundamental Ganita template which was adopted by all these great practitioners. Toward this, we start with an algorithmic interpretation of Prajapati’s efforts to create a stable, self-organized universe [9].

Prajapati’s Algorithm

Prajapati employs an algorithm to create the cosmos. An iteration in this algorithm consists of an experimental trial, followed by an observation of the output data, which triggers a review and validation phase, followed by an adjustment of ‘design parameters’ and re-trial, if necessary. This process converges to Prajapati’s satisfaction within three iterations. However, no attempt is made to prove or claim with absolute certainty that among all possible universes, his is the most perfect and infallible. Since time is cyclical, such universes are dissolved and recreated with no beginning or end. The Rig Veda explicitly recognizes the inherent uncertainty associated with any answer to such questions [10].

1. The first empirical trial produces a cosmos which is observed to be full of entities too similar in nature and they simply merge into each other, so that there is practically nothing to unite.  This is a homogeneous and ‘over-ordered’ universe where there is nothing left to know, and this system quickly becomes unmanageable. From a statistical perspective, there is little or no variance in this first universe.
2. Prajapati increases variability in his second try but the output shifts to the other extreme. The world is now way too heterogeneous and there is no commonality between beings to relate to, and to unite. Nothing is certain and can be known, and chaos reigns.
3. Learning from the first two attempts, Prajapati is able to achieve a good balance in his third version that overcomes prior problems, and the algorithm terminates with a stable universe.

How does Prajapati accomplish this task? In his book ‘Being Different’, Rajiv Malhotra says “Prajapati recognizes that all life should be situated between these opposing excesses of too much identity difference and too much homogeneity. Ultimately, he succeeds in producing just such a universe. He does so through the power of resemblance, known as ‘bandhuta’ or bandhu, which was discussed in Chapter 3. The Vedas abound in attempts at finding connections among the numerous planes of reality. This serves as a cardinal principle of all Vedic thought and moral discourse”.

Every entity created is unique, while also bearing some form of resemblance to each other.  Some resemblances may be more easily spotted, while others may be subtle and identifiable only after considerable effort. These Bandhus are the ‘conceptual linkages and tenuous associations’ revealed to Ramanujan after intense tapasya, and he is able to find “union in what others saw as unrelated” because the cognizable world is mirrored and mapped into the transcendental world, and vice versa via these Bandhus [11]. These strands of resemblances intertwine the elements of the universe into an integral unity, where every individual element’s identity is real but provisional, while always being rooted in the independent whole. There are no separately independent realities for individual elements and the methods of Ganita mirror Prajapati’s algorithm.

Bandhu

"The bandhus represent the laws that hold the universe together (Vishnu), paroksha is the dance of consciousness that is ever changing (Shiva), and Yajna is the process of
 change (Devi)" - Subhash Kak, Pragnya Sutra [PS, 12].

The idea of ‘resemblance’ is fundamental to the acquisition of knowledge that is required to make ‘risky’ and useful predictions about the future with a measure of confidence. This concept can be illustrated using the analogy of a modern business forecasting system. Suppose a company launches a brand-new product in the market and needs to know now how many units it is likely to sell in the next 6-12 months. Since no prior sales data about this product is available, no statistical method cannot be employed to directly calculate this number. To overcome this limitation, the new product A is mapped in terms of its selling attributes to that pre-existing product B which it resembles most. B’s data is borrowed to generate an initial sales forecast for A. Machine learning and AI techniques can be used to learn such recursive patterns, even deep ones, from unstructured data.

However, a machine has its limits. Computer Scientist and Sanskrit scholar Prof. Subhash Kak notes [12] “… knowledge emerges from a familiarization with its inner space and it may be seen to be a consequence of the bandhus (bonds) that exist between the outer and inner worlds. If there were no such bandhu, it would be impossible to make sense of the world. Machines only follow predefined rules and they don’t have bandhus, which is why they cannot be conscious. The bandhus are the ground that make awareness possible“.

Bandhus can be in the form of numbers, biological rhythms, sounds, lights, touch, etc.[11]. Or via Meghadutam? A study of the applications and motivation of ancient Indian geometry reveals the traditional Hindu approach of coexisting in harmony and synchronizing with nature by recognizing certain auspicious and sacred ratios and numbers (e.g. 108).  Two examples are stated below, which also bring to light the continuity and commonality in thought between the Harappan and Vedic time periods. We will discuss this in depth later in our series.

1. The ratios and measurements used in Harappan architecture at Dholavira (2500 BCE or earlier)
2. The dimensions and numbers of bricks used in Vedic fire altars.

Two of the three key notions of dharmic cosmology are recursion and paradox [11]. The former, via the principle of resemblance, injects a sense of order and certainty into our view of the transactional world, whereas the latter preserves the mystery and uncertainty about the true nature of ultimate reality. It is convenient in the Ganita context to understand this recursion using the Vedic metaphor of Indra’s net.

Self Organizing Patterns: Vedic Metaphor of Indra’s Net

"The Vedic deity Indra is said to have an infinite net consisting of a jewel in each node, arranged so that every jewel reflects all the other jewels; there is no separate self-existence of any jewel. Each is unique in its reflection of all others. Indra's Net symbolizes a universe with infinite dependencies and relations interwoven among all its members, none of which exists apart from but only in the context of this collective reality."  - Rajiv Malhotra, Indra's Net.

The links in this self-organized network are precisely the Bandhus. Since the ultimate reality is like Indra’s Net, Prajapati’s world allows order and information to emerge from what appears to be nothing but chaos and uncertainty (even soccer matches!). Such an Indra’s Net becomes a limitless source of useful ideas for Ganita. We provide three examples from Mathematics to illustrate this.

• The ‘Rule of Five’ [14] states that: “There is a 93.75% chance that the median of a population is between the smallest and largest values in any random sample of five from that population.” Just five random samples are enough in nature, with no preconception about its probability distribution, to achieve a significant reduction in uncertainty – from being totally unsure, to knowing a lot about any group’s median behavior. This order has been hiding all along in plain sight.
• The world around us is full of (approximately) normal distributions or bell curves, allowing a certain statistical order to emerge out of seemingly disorganized groups.

  

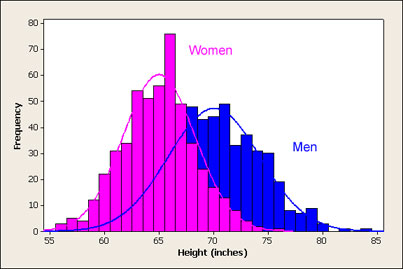
  Of course, not everything in nature is normally distributed. There are plenty of exceptions [14]. In [15], Lyon tries to understand how such normal distributions come about in nature. He argues that it is not because of the central limit theorem. He uses inference (which Indian logicians recognize as anumana) to understand how these patterns are generated in nature. By using the idea of ‘entropy’ to denote the degree of chaos (or disorder), we learn: “A further fact, which serves to ’explain’ why it is that this ’order generated out of chaos’ often has the appearance of a normal distribution, is that out of all distributions having the same variance the normal has maximum entropy (i.e. the minimum amount of information).” The balance between order and chaos in nature produces approximate bell curves, whose statistical properties can be gainfully employed to better understand this world. Sometimes, this Indra’s Net manifests itself as spectacular visuals.

• In the brief video below, we can observe fireflies synchronizing. Thousands of fireflies light up at the same instant by simply doing their Dharma of flashing ‘strobes’ and sending out a visual signal, and in turn appropriately responding to incoming signals [16]. This was first noticed by western researchers in the jungles of Thailand. After the first sync-up, they remain synced. Self-organization is quite natural in the Vedic universe, and now we are beginning to see rigorous mathematical proofs reaffirming this reality. Inference and intuition was used by mathematicians in tandem with logical reasoning to understand the process of ‘sync’ and prove that synchronization is guaranteed in nature under certain conditions. Strogatz notes in [16] “The implication is that in a population of fireflies or brain cells, the oscillators have to be similar enough or nobody will synchronize at all.”  A certain balance between order and chaos is required for sync, and evidently, this is not uncommon in nature. After all, the dance of the universe is synced to the dance of Nataraja. Out of these self-organization principles emerge the beautiful equations and results of Ganita.

The Ganita of self-organization shows up prominently in Hinduism and in India. This decentralized ‘sync’ by insects could be quite naturally viewed by Hindus as a firefly Kumbh Mela. Pre-colonial India was largely decentralized. Self-organization reduces transactional costs and is environment friendly. Hinduism’s resilience and even a degree of ‘antifragility’ are due to built-in error-correcting mechanisms and the ability to constructively balance order and chaos [10]. The fidelity of Vedic chants has been orally preserved over several thousand years via embedded  layers of data redundancy that resemble ideas within modern methods of information transmission over a noisy communication channel. In the video below, Manjul Bhargava provides an example of Ganita in Sanskrit Kavya, which embeds an error-correcting code.

Several notoriously hard-to-solve mathematical problems (see example picture below) recognized in computational complexity theory are routinely managed in practice. Problem instances that actually manifest in nature appear to have certain data patterns and organization that allow them to be solved fairly quickly to the level of accuracy required by the practical application.

Along with resemblances and patterns in nature comes paradox. Per Subhash Kak [11], “paradox is the recognition that the bandhu must lie outside of rational system, leading to the distinction between the “higher” science of consciousness and the “lower,” rational objective science“.  How does Ganita deal with paradox and uncertainty?

Ganita: At Ease With Uncertainty

A bit beyond perception’s reach

I sometimes believe I see

that Life is two locked boxes, each

containing the other’s key. 

—Piet Hein

(and in the words of Clint Eastwood, “If you want a guarantee, buy a toaster“).

In the Vedic period, there used to be enigmatic exchanges between scholars, known as Brahmodya, where a riddle about the nature of ultimate reality (Brahman, in Hinduism) was posed. The respondent remained silent if they could not decipher it, or countered with a deeper riddle if the hidden Bandhu was recognized [17]. (An entertaining version of this contest is the silent exchange via hand-gestures between Kalidasa and the scholar-princess Vidyottama). Dharma traditions recognize that our understanding of reality is likely to be incomplete. For example, Rajiv Malhotra notes in [10]: “There is equivalence in the relationship between sunya (emptiness) and purna (completeness or integral wholeness), the paradox being that the void has within it the whole“. With new knowledge and its associated benefits invariably comes uncertainty and ‘side effects’. There is no ‘free lunch’. Consequently, man-made algorithms are not infallible and dharma systems explicitly factor this in.

It is well known that Smritis have to be updated periodically while always serving  the unchanging Shruti.  Similarly, Ganita practitioners come up with increasingly better Siddhantas that progressively improve our understanding of natural phenomena. What is also important to remember is that the Indian approach to any field, including Ganita, is one of shraddha that is grounded in the sacred. We can be transformed by this experience and attain higher levels of consciousness that bring us ever closer to experiencing the ultimate reality.  This view is apparent in Aryabhatiya [5]: “the end of learning was the attainment of the Supreme Brahman and this could be easily achieved by the study of astronomy. In the closing stanza of the Dasagitikasutra, he says: “Knowing this Dasagitikasutra, the motion of the Earth and the planets, on the celestial sphere, one attains the Supreme Brahman after piercing through the orbits of the planets and the stars“.

The Integral versus the Synthetic Approach

We briefly compare two alternative approaches to dealing with paradox and uncertainty:

1. Integral approach
   • Recognize reality with all its inherent diversity as is, as the ideal, and treat knowledge acquisition as a systematic process of reducing uncertainty.
   • Inference and intuition is useful in gaining new knowledge, and ingenuity is prized in such a tradition. Such knowledge is fallible, and new and improved methods are continually developed to reduce error to an acceptable level. Pragmatism rules, and the layman is familiar with the Ganita required for his/her own profession [2].
   • The validity of a method is demonstrated via Upapattis [1] that are rooted in reality.  From a logic perspective, the validity of knowledge is tied to the specific Pramanas it relies on, which may not be universally acceptable.
2. Synthetic approach [10, 3]
   • Reject chaos as undesirable and consider ‘perfect order’ to be the ideal, and reality as subservient to this ideal ‘model’.
   • This binary mindset prefers to view reality as a bunch of separately independent systems where knowledge acquisition is preferably beyond doubt and free of empiricism.
   • Every new result is proven conclusively and universally using logic, starting from a minimal number of ‘self-evident’ axioms.

This distinction does not automatically imply that Ganita (example of integral approach) and modern science/math (largely synthetic approach) are in a state of irreconcilable conflict. As Roddam Narasimha notes [24]: “Modern science seems to have acquired, perhaps by fortunate accident, the property that the great Buddhist philosopher Nagarjuna called prapakatva: i.e., it delivers what it promises; it may not be the Truth, but it is honest“. What is undeniable and supported by fact is that by the 16th century CE, Ganita results had already laid the foundations for many crucial developments in modern science and mathematics [3].  Ramanujan is an example of an Indian who practiced the integral approach, and found a way to work constructively with western mathematicians so that his results could benefit the world.

It is interesting to see how Mathematician Hardy and Ramanujan reacted to each other’s approach as noted in [8].

1. When Hardy asked for proof, we excerpt Ramanujan’s response: “…. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter. You may ask how you can accept results based upon wrong premises. What I tell you is this: Verify the results I give and if they agree with your results, got by treading on the groove in which the present day mathematicians move, you should at least grant that there may be some truths in my fundamental basis.“
2. Professor Hardy’s description of Ramanujan’s approach: “It was his insight into algebraic formulae, transformations of infinite series and so forth, that was most amazing. On this side most certainly I have never met his equal, and I can compare him only with Euler or Jacobi. He worked far more than the majority of modern mathematicians, by induction from numerical examples; all his congruence properties of partitions, for example, were discovered in this way. But with his memory, his patience and his power of calculation, he combined a power of generalisation, a feeling for form, a capacity for rapid modification of his hypothesis, that were often really startling, and made him, in his own peculiar field, without a rival in his day.”.  Prof. Hardy was careful not to tamper with Ramanujan’s mysterious ability, which was rooted in Ganita.
3. On Ramanujan’s approach to the partition problem: “… the uncanny accuracy of their results attested to the power of the approximating technique they had used to get them ..So subtle and inspired were the approximations it permitted that it went beyond approximation to promise exactitude. …. Selberg, in fact, argues that Hardy’s insistence on certain methods of classical analysis actually impeded their efforts; and that lacking faith in Ramanujan’s intuition he discouraged a search for the kind of exact solution Rademacher produced twenty years later.”

Commentators have often termed this integral Indian approach as ‘Paninian’. We try to better understand what they mean by that.

The Real is the Ideal, and the Perfect is its Approximation

If the west has Euclid as the pioneer and exemplar for mathematics, India follows Panini. In [18], Dr. J. J. Bajaj explains this statement by using the commentary of Patanjali on Panini’s work: “In providing this characterisation of the science of grammar Patanjali laid his finger on perhaps the most essential feature of the Indian scientific effort. Science in India seems to start with the assumption that truth resides in the real world with all its diversity and complexity… As Patanjali emphasises, valid utterances are not manufactured by the Linguist, but are already established by the practice in the world. Nobody goes to a linguist asking for valid utterances, the way one goes to a potter asking for pots. Linguist do make generalisations about the language as spoken in the world. But these generalisations are not the truth behind or above the reality. These are not the idealisation according to which reality is to be tailored. On the other hand what is ideal is the real, and some part of the real always escapes our idealisation of it. There are always exceptions. It is the business of the scientist to formulate these generalisations, but also at the same time to be always attuned to the reality, to always to conscious of the exceptional nature of each specific instance. This attitude, as we shall have occasion to see, seems to permeate all Indian science and makes it an exercise quite different from the scientific enterprise of the West.”

This discussion tells us that Panini’s is an integral approach rooted in the ultimate reality. On the other hand, the synthetic approach mentioned is popular in the west. Advances in modern science have been attributed to this approach. However, this approach can allow false assumptions to creep if the reality-check step is missing. There is an interesting story about the US Air Force set in the 1950s when they discovered that many of their pilots were losing control of their planes and crashing at an alarming rate.

The investigation eventually narrowed down the cause to the design of the cockpit, which was precisely engineered to a precise standard in the 1920s for the average American pilot. The USAF theory was that the average pilot had gotten bigger in the prior three decades and so the cockpit dimensions need to be re-sized upward. More than 4000 pilots were measured across 140 dimensions to compute a new standardized design. During this process, an analyst who was sifting through this data discovered that the total number of pilots who were average or near-average across these dimensions was exactly zero.  The ideal pilot simply did not exist.

A similar survey was conducted a few years earlier to find a lady in Cleveland who would closely match the ideal normal figure (‘Norma’). Among the nearly 4000 contestants, there was not one lady in the survey who matched Norma’s perfect vital statistics. Assuming that reality will conform to a non-existent ideal model is a recipe for disaster. USAF quickly realized that it was far better to design and periodically update designs based on the observed reality by explicitly taking uncertainty into account. This is exactly what the USAF did thereafter and switched their cockpit design philosophy to ‘individual fit’. It was a pragmatic response to an important problem that was jeopardizing pilot safety and costing millions of dollars. From an Indian perspective, the USAF chose the Ganita approach. Every US military branch embraced this idea soon after. A similar revolution is ongoing in healthcare, with allopathic medicine representing the synthetic alternative, and Ayurveda being the integral method. This integral approach to computing produced amazing results such as the decimal place value system and Algebra.

Integral Unity of Indian Place Value System

The Indian decimal place value system that is now used all over the world is startlingly simple and elegant. It arises from the sacred idea of ‘the One that manifests as many’ that exists in all Dharma thought systems (and Aryabhatiya paid obeisance to). Just like Panini was able to encode the infinite possibilities of pre-existing and all future utterances using a small number of rules, the Indian place value system too can represent all previously used and yet-to-be-used numbers in the universe using just a few symbols and rules.  Every digit in an N-digit number is denoted by its symbol that has a provisional reality, and through an established place value, it acquires a manifested form that unites into the whole number. As shown in the picture below,  some two thousand years ago, Rishis explain that the same symbol ‘1’ can realize different values, e.g. in the unit, tens, and hundreds place just as a lady can be a daughter, sister, mother, etc.

Algebra and Sanskrit

The place value system is essentially algebraic in nature. Bijaganita (Algebra via Arabic Al-Jabr) is a natural extension of this idea that arose independently in India (early algebraic results can be found in the Sulvasutras[1]). Here a single symbol like ‘x’ represents an unmanifest quantity that can potentially take one of many values. It eventually takes a fixed numerical value that is feasible to the equations representing the reality which it is part of. In [10], we find this algebraic concept mirrored in Sanskrit [10]: “When a word with a contextually determined meaning is reduced to only one of its many meanings, it is akin to assigning a specific constant value to an algebraic variable, thereby eliminating its usefulness as a variable.”

These context-sensitive meanings in Sanskrit, and the Contextual and Universal Dharma ethics are other well-known concepts that resemble this idea. For example, the word ‘Lingam’ which means symbol or icon has multiple contextual meanings [10]. The idea of equations and the introduction of a symbolic processing language to manage such equations also existed in India. The Bakshali manuscript provides evidence of this [6]. Aside from the decimal system, there were also the Katapayadi, Bhutasamkhya, and the Aryabhata notation that encoded numerical data in exquisite sacred verse [1]. Here are some bewitching examples.

This Paninian approach naturally motivates the generation of permutations and combinations while are fundamental to the idea of mathematical ‘probability and chance’, and finds application in Sanskrit Kavya [3]. The infinite-series results achieved by Madhava of the Kerala school long before McLaurin/Taylor/Leibniz, etc. also resemble this generating principle. The game of chess (Chaturanga), and snakes and ladders (Moksha Pata, Vaikuntapalli), etc. also have a similar structure and not surprisingly, originated in India. German Sanskritist Paul Thieme noted that a civilization that produced Paninian grammar could easily have produced also the game of chess, which it did [4].  The potential chaos that can arise from permitting multiplicity is ingeniously managed via the guiding principles of Dharma to produce harmonious order. All these discussions raise an obvious question – why are Indians so ‘tuned in’ to this integral approach?

Forest Civilization’s Pattern Seekers and Algorizers

The multiplicity of numbers, cascading permutations, infinitesimals running amok, and the never ending decimals of irrationals seemingly paralyzed the binary mindset at one point in time. On the other hand, this chaotic prospect caused little anxiety among the ancient Indians who were grounded in Dharmic view where such diversity are but natural forms of the One. In general, the practice of Ganita is appealing to those who seek recurring patterns and inter-connections in nature.

India is a forest civilization [10]. A significant portion of the narrative in two of its major works of Itihasa, the Ramayana and the Mahabharata, occur in the forest, which is a complex ecosystem where the inter-dependency of its members is Omnipresent.  It is but natural that the Indians are attracted to the infinitely repeating patterns that abound in nature and draw inspiration and inferences from them. On the left is a picture of the tessellations drawn by ancient Indians on rocks [19] several thousands of years ago (possibly upper Paleolithic period. This may remind some of Kolams). On the right is a visualization of the theta function [20] that Ramanujan may have studied while coming up with his equations for the ‘mock theta’ functions that he made famous.

Based on an intuition and deep contemplation about certain connections and resemblances observed in nature, a Ganita expert comes up with a sequence of calculations. Scientist Roddam Narasimha describes this Indian approach [24] as that of pattern seekers and algorisers and that the Indian astronomer (like Aryabhata) can “discern patterns in planetary motion and make computations, and proceeds to devise clever algorithms to carry out such calculations“. He describes the Indian approach via the following sequence: observation →  algorithm → validated conclusion. Several Sanskrit keywords are used within this approach, for which no exact English equivalent word exists. We briefly summarize these keywords based on the discussion in [6].

Key Ganita Non-Translatables

Pramana – correct cognition, a means of acquiring valid knowledge. Pratyaksha and Anumana are two important Pramanas in Ganita.

Anumana – inference, the key reasoning component in Indian logic. This is not the same as deduction, but is a derived conclusion from the observation of patterns.

Pariksha – careful comprehensive observation. e.g. yantra pariksha:  observation using instruments. An extension of Pratyaksha (direct observation and perception), the oldest and most universal Pramana among darshanas.

Drg-Ganita –  ‘seeing and computing’. This is an important method introduced by Parameshwara of the Kerala school, which looks for agreement between what was computed and what is observed.

Siddhanta – a validated conclusion, or a validated algorithmic package. What happens when there is a clash between Siddhantas? In [6], “Nilakantha recommends that under such  conditions more observations need to be taken with instruments and compared with calculation, and that the numerical parameters should be changed (or the algorithms tuned) so as to improve agreement. In other words a new siddhanta has to be created. Siddhantas are thus human creations, and the best at any time may not remain
so for long—it is valid only for some finite periods of time.”

Yukti – skilful and ingenious practice. Ganita gives the pride of place to Yukti, sometimes overruling the primacy of the Agamas. Verse (2.5) from the Bhagavad Gita says “yogah: karmasu kausalam“, yoga is skill in action [6].  It appears that the Ganita tradition had little time for ‘pure’ theorists who lacked the Yukti or intent to deliver realizable results.

Anveshana – ‘wild goose chase’. In general usage, this word has a positive connotation but in the context of Ganita it represents a futile exploration.

Upapatti – a rigorous validation of results to the satisfaction of peer experts. Yukti is employed to constructively demonstrate how a result can be correctly reproduced by anyone else. This is not the same as the synthetic notion of abstract proof [1]. An important book in this regard is the Ganita Yukti Bhasa of Jyeshtadeva hailing from the Kerala school. It is a myth that Indian mathematicians provided no proof of their results. One has to read the accompanying commentaries on the results stated in Sutra form in order to understand all aspects of a Ganita result, including the validation step. The tradition of providing Upapattis is an old and well established one [22].

We conclude this introductory post by excerpting some passages from an essay on Mathematics by Henry Poincaré. In this essay, we get to read his independent views on the nature of reality. He also provides a balanced discussion of the pros and cons of different approaches that can be employed to generate new results. It is worth comparing his views with the ancient Indian perspective. This discussion also sets the stage for the next blog in this series.

Poincaré on ‘what is reality?’

We excerpt a couple of paragraphs from a 1905 essay [21] by the great French mathematician Henri Poincaré. From a Dharma and Ganita perspective, Poincare alludes to the integral unity of reality rather than a synthetic ‘artificial assemblage’. He also talks about the need for a ‘direct sense’ of the internal unity of a piece of reasoning in order to possess the ‘entire reality’. He also uses the principle of resemblance to explain his ideas.

“The physiologists tell us that organisms are formed of cells; the chemists add that cells themselves are formed of atoms. Does this mean that these atoms or these cells constitute reality, or rather the sole reality? The way in which these cells are arranged and from which results the unity of the individual, is not it also a reality much more interesting than that of the isolated elements…?“

Well, there is something analogous to this in mathematics. The logician cuts up, so to speak, each demonstration into a very great number of elementary operations; when we have examined these operations one after the other and ascertained that each is correct, are we to think we have grasped the real meaning of the demonstration? …. Evidently not; we shall not yet possess the entire reality; that I know not what which makes the unity of the demonstration will completely elude us.”

“…often a very uncommon penetration is necessary for their discovery. The analysts, not to let these hidden analogies escape them, that is, in order to be inventors, must, without the aid of the senses and imagination, have a direct sense of what constitutes the unity of a piece of reasoning, of what makes, so to speak, its soul and inmost life. When one talked with M Hermite, he never evoked a sensuous image, and yet you soon perceived that the most abstract entities were for him like living beings. He did not see them, but he perceived that they are not an artificial assemblage, and that they have some principle of internal unity.”

---

What we don’t know about India’s Ganita heritage is much more than what we currently know. Only a minuscule fraction of primary source texts of Ganita have been studied and interpreted so far. We have to thank researchers like the late K. V. Sarma for their tireless work in this regard.

"Our youth are hungry for a sensible knowledge of our past, but are denied an opportunity to acquire it by a marvellous educational system that shuns history in science curricula, and by the paucity of attractive but reliable accounts of the fascinating history of Indic ideas. Our academies, universities, museums and other institutions need to make such a project a national mission. Anything less would be irrational blindness to a unique legacy." - Roddam Narasimha [23].

Acknowledgment: I thank the ICP editor and bloggers for their constructive feedback and corrections.

* Indic epistemology traditionally places Ganita under Jyotisha. The original quote in Vedanga Jyotisha refers to Jyotisha in its enlarged meaning, hence the popular direct translation today of that word as referring to 'Math', used above as Ganita.

---

References

1. Indian Mathematics: An Overview, Video Lecture by M. D. Srinivas.
2. Mathematics Education in India: Status and Outlook. Editors: R. Ramanujam, K. Subramaniam. Homi Bhabha Centre for Science Education, TIFR. 2012.
3. Cultural Foundations of Mathematics: The Nature of Mathematical Proof and the Transmission of the Calculus from India to Europe in the 16th c. CE., C. K. Raju, Pearson India. 2009.
4. Vilasamanimanjari: a 19th century chess manual in Sanskrit. Shrinivas Tilak. 2011.
5. Aryabhatiya of Aryabhata. Critically edited with Introduction, English Translation. By
   Kripa Shankar Shukla, in collaboration with K. V. Sarma. 1976.
6. Epistemology and Language in Indian Astronomy and Mathematics. Roddam Narasimha. Journal of Indian Philosophy (2007).
7. Tantrasangraha of Nilakantha Somayaji (Culture and History of Mathematics) Bilingual Edition. by K. Ramasubramanian and M. S. Sriram. Hindustan Book Agency. 2011.
8. The Man Who Knew Infinity: A Life of the Genius Ramanujan. Robert Kanigel. Charles Scribner’s Sons, NY, NY. 1991.
9. Reflections on Resemblance, Ritual, and Religion. B. K. Smith. Oxford University Press, New York. 1989.
10. Being Different: An Indian Challenge to Western Universalism. Rajiv Malhotra. Harper Collins. 2011.
11. Art and Cosmology in India. Subhash Kak. Patanjali Lecture given at Center for Indic Studies, University of Massachusetts, 2006.
12. The Pragnya Sutra: Aphorisms of Intuition. Subhash Kak. Baton Rouge, 2006.
13. Indra’s Net: Defending Hinduism’s Philosophical Unity. Rajiv Malhotra. Harper Collins. 2011.
14. How to Measure Anything: Finding the Value of Intangibles in Business. 3rd Edition. Douglas W. Hubbard. Wiley. 2014.
15. Why are Normal Distributions Normal? Aidan Lyon. British Journal of the Philosophy of Science. 2013.
16. Sync: How Order Emerges from Chaos In the Universe, Nature, and Daily Life. Steven H. Strogatz,Hachette Books. 2012.
17. Abhinavagupta’s Conception of Humor, svabhinava.org.  Sunthar Visuvalingam.
18. The Indian Tradition in Science and Technology: An Overview. J. J. Bajaj. PPST Bulletin. www.samanvaya.com.
19. Computing Science in Ancient India. T. R. N. Rao and Subhash Kak. Center for Advanced Computer Studies. University of SW Louisiana. 1998.
20. Ramanujan’s Mock Modular Forms: Indian Mathematician’s Dream Conjecture Finally Proven. Huffington Post Science 2012.
21. Intuition and Logic in Mathematics. English Translation of Essay by Henri Poincaré. 1905.
22. Ganita Yukti Bhasa: Rationales in Mathematical Astronomy of Jyeshtadeva. Vol 1. Malalayalam text critically edited with English translation by K. V. Sarma. 2008
23. The ‘historic’ storm at the Mumbai Science Congress. Roddam Narasimha. Guest Editorial, Current Science, Vol 108 (4), 2015.
24. Some thoughts on the Indian half of Needham question: Axioms, models and algorithms. Roddam Narasimha. 2002.
25. Subbarayappa, B.V. , Indian astronomy: a historical perspective. In: Biswas, Mallik, Vishveshwara (eds.), “Cosmic Perspectives”, Cambridge University.1989.