The Great King Suchi of Magadha
His calendar was a royal mess
because the equinoxes precess
until he learned 'the lore of time' from Sage Lagadha.

Jyotihsastra

Jyotihsastra is the ancient Indian ‘science of light’ [2]. It includes within it the field of astronomy, which was known as Nakshatra Vidya (the science of the stars). Jyotihsastra is used for dik-desa-kala nirnaya (triprasna), i.e. to determine (direction, location, time) [4]. The Vedanga Jyotisha is an ancient text focused on Jyotisha, one of the six Vedangas. The Vedic texts, including the Upavedas and Vedangas, are harmoniously interlinked into an integrally united knowledge system. No one part of this system can be properly understood through an isolated study [1]. A key purpose of the Vedas is the performance of Yagnas correctly and on time. Time-keeping is the goal of Vedanga Jyotisha.

We resume our study of Ganitasastra at ICP through an inquiry into Jyotihsastra. This post is not an exhaustive restatement of facts. Instead, we try to understand the motivation and intuition behind the Ganita features of Vedanga Jyotisha (VJ). The Shulbasutras, which are part of the Kalpa Vedanga are also rich in Ganita, and will be discussed separately.

College students asked a professor 'Sir, what is time?' who replied "I can tell you what is the time, but I cannot tell you what is time"[4].

Vedanga Jyotisha

VJ is the earliest extant Indic work on time-keeping in the form of a handbook that is devoted to Kalavidhanasastra, the science of time-keeping. It provides the calculations associated with a lunisolar calendar derived from the Brahmanas and the Vedic Samhitas. VJ is not a self-contained treatise and any missing definitions, unstated assumptions, etc., are to be inferred from prior Indic sources and commentaries [1].

Vedanga Jyotisha has absolutely nothing to do with Phalita Jyotisha or Astrology [11]. 

The VJ was compiled around 1350 BCE (between 1150-1550 BCE) and is attributed in its verse to Lagadha, and key ideas in the VJ have been shown to belong to the Vedic texts and derived from earlier periods. VJ is in verse form while the other 5 Vedangas (Nirukta, Chandas, Kalpa, Vyakarana, & Siksha) are in Sutras indicating that it is the earliest of the six [1]. VJ was neither the first nor the last word in Indic time-keeping and astronomy as the Indians continued to make pioneering contributions to Ganita and Jyotihsastra over three millennia. These techniques enabled the Indics to produce a stable working calendar that could be employed for diverse purposes, and was sought after by the rest the world. The ancient Indic calendar traveled to China, and many other places [11].

VJ is available in the form of two ‘rescensions’ denoted as Rigveda Jyotisha (Arca Jyotisha, RVJ, 36 verses, earlier version) and Yajurveda Jyotisha (Yajusa Jyotisha, YVJ, 43 verses), which significantly overlap. Deciphering these rescensions turned out to be a challenging task. This effort started in the 1830s, culminating in the authoritative work of Prof. Kuppanna Sastry [1] in the 1980s who succeeded in meaningfully explaining all verses. Virtually every contemporary study of VJ cites his scholarship.

Time-keeping traditions of India

https://indicportal.orgvedic-cosmology-the-dharmic-view-of-time/

We will devote considerable space discussing the unbroken traditions of astronomy and time-keeping that preceded Vedanga Jyotisha.

The Indic approach to discovery quite naturally arises from Rta, the cosmic order that is an expression of Satya, the ultimate reality. This cosmic order is experienced at every level from the microcosm to macrocosm. Time is sacred in this cosmology, and we have the kalachakra representing cyclic time, and it is intuitive that elapsed time can be tracked using precisely recurring rhythms of different durations that abound in nature. 18th century British scientist John Playfair who studied Hindu time-keeping in a manuscript obtained from Thailand, wrote an extensive treatise and was amazed by the Indic conception of cyclical nature [8]. He made several other important observations, which can be found within the cited references.

The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom. 
- Physical Measurement Lab at NIST

Our solar system is quite flat, and hence the moon and most of the planets are located in a narrow region around the ecliptic, the apparent path of the sun in the sky during the day. This is really convenient for observation since it eliminates the need to focus on the innumerable luminaries that are away from the ecliptic. The moon’s path is within 5% of the ecliptic. The Ancient Indics kept time based on the periodicity of the (apparent) motion of the sun and the real motion of the moon. The study of planetary movements was not necessary to achieve this goal and does not concern VJ.

why isn't there a solar eclipse every New Moon night?

Careful observation was a critical component of Vedic astronomy and this became the hallmark of the Indic approach to discovery and obtaining valid knowledge in general, where all schools of dharma unanimously accept Pratyaksha Pramana [11]. From the perspective of accurate time-keeping required for Yagnas, kalavidhanasastra is a pratyaksha sastra [4], and is not deduced from a ‘black box’ math model.

By the early Rig Vedic period, one or more calendars were already in use for managing day to day activities. Time-keeping is critical for agricultural planning, e.g. to coordinate activities associated with the beginning and end of seasons, and continues to be important to the Indian economy [11].

The earth's equatorial plane is tilted at an angle of 23.5° with respect to the ecliptic plane. This results in varying seasons and daylight hours.

The Vedic people knew about the solstices and employed a six-season calendar which is special to India (it included a rainy season: Varsha Rtu with months Nabha and Nabhasya). Obviously, the ability to accurately predict the arrival date of monsoons has always had significant economic value in India. The twelve tropical months along with their seasons in the Yajurveda are [2]:

Madhu, Maadhava in vasanta (spring),
Sukra, Suci in greeshma (summer),
Nabha, Nabhasya in varshaa (rainy),
Isa, Urja in sarada (autumn),
Saha, Sahasya in hemanta (winter), and
Tapa, Tapasya in sishira (freezing).

In 2004, agricultural operations were mistimed in India. Why? The monsoon was officially considered 'delayed' in the government calendar. In reality, it arrived on time per the traditional Indic calendar [11].

The trinity of adhidaiva, adhibhuta, and adhyatma are integrally united via Bandhus in the Vedic knowledge system [2, 9].  There exists a deep and ancient connection between Yagna (‘ the workshop where Bandhus are forged between the microcosm and macrocosm’ [9]) and time-keeping. Knowledge of the luminary phases was used to ensure that the monthly (Darshapuranamaasa) and seasonal (Chaturmasya) Yagnas were performed at the correct times [3]. The Atri family priests had the knowledge required to predict solar eclipses. By the time of the Yajurveda, the Hindus knew that a solar year was slightly more than 365 days. And importantly from a VJ perspective, a five year Yuga was already known, along with the need for two intercalary months to complete a Yuga [1].

pic source. By careful and patient daily observation of the sun at the same time in the sky, one can find out when the solstices occur (‘when the sun stands still’).

Prajapati as Time

Prajapati the creator is central to Vedic tradition. In his book ‘Being Different’, Rajiv Malhotra quotes the Rig Veda: “yajna is the very navel of the universe. It was Lord Prajapati who first fashioned yajna, and through it he wove into one fabric the warp and weft of the three worlds (Rig Veda I,164,33-35).” [9]. Prajapati creates and embodies a self-sustainable, self-correcting universe using the correspondence principle of bandhuta to achieve a balance between homogeneity and heterogeneity [9]. Prajapati is time, the very creator of the Vedas, signifying that the knowledge within the Vedas has no beginning or end [2]. He is Rta, the cosmic rhythm moving in a spiral, which indicates the Kalachakra, cyclical time [14].

Prajapati and Yagna are central to Vedanga Jyotisha, and receive the first respects in the starting verses of the VJ. The natural periodic events such as seasons, days, etc. are the five limbs of Prajapati, who personifies and presides over the five-year Yuga [1]. The separated faculties and limbs of Prajapati unite to form the infinite diversity of the universe, and the Yagna becomes a time-design to unite this multiplicity and continue the cosmic rhythm [14]. This five year Yuga is mirrored in Yagna through the constructed five-layered Agnicayana altar [6]. The Aahavaniya altar is built using 396 bricks that represent the days of the year: 360 to represent the Vedic ritual year and an additional 36 to represent the thirteenth (intercalary) month [3]. Many such bandhus arise through Yagnas [2]. The five-year Yuga is also a feature of Jain astronomy [6].

VJ states that those who correctly understand the effect of time on movements of the luminaries in the sky can fully grasp the impact of the Yagnas. One who truly understands the Vedas and Vedanga Jyotisha can experience transcendental bliss. These verses underline the integral unity [9] of the outer-material and inner-spiritual realms. We can see this dharmic concept re-asserted two thousand years later in the initial verses of Aryabhatiya, and more recently in Ramanujan’s approach as well.

The Indics were more than pattern seeking enthusiasts; they sought within patterns the deepest unity underlying nature’s diversity, and from this emerged the Yuga.  Yaga, Yoga, and Yuga (or the 3 Ys, with apologies to Modi ji) – all have a root meaning ‘to unite’. In [13], Prof Subhash Kak notes: “the ancient Indian calendar is an attempt to harmonize the motions of the Sun and the Moon…. Yoga may be seen as the harmonization of the motions of the inner planets of the body.  Patanjali’s Yoga Sutra speaks of how meditation on the Sun reveals the nature of the world-system and meditation on the Moon and the Polestar reveals the arrangement and the motion of the planets and the stars. Such assertions imply that turning inward can provide insights.”.

Nakshatras in Vedic Tradition

Since the most ancient time, Hindu astronomy adopted the sidereal system. This was done implicitly using Nakshatras (stars or asterisms) in the Vedic period, and explicitly in the VJ, as well shall see later [16]. The Vedics used 27 Nakshatras in the vicinity of the ecliptic to track the lunar passage where the moon takes 27.32 days to return to a fixed reference point (sidereal lunar month). To identify the Nakshatra location of the sun, a heliacal rising and setting of a Nakshatra seems to have been employed, i.e., a Nakshatra may be visible near the horizon just before sunrise or sunset.  Texts point to a multi-disciplinary approach to Jyotisha employing a Nakshatra Darsha (expert observer/astronomer) and Ganaka (a calculation expert). The term ‘Nakshatra Vidya’ is mentioned in the Chandogya Upanishad [2].

Mentions of Nakshatra observations in ancient texts are useful because they allow us to date these events using the earth’s precession rate. For example, Kuppanna Sastry quotes the Satapatha Brahman, mentioning that ‘the asterismal group Kritika never swerve from the east while others do’, which was also confirmed by the commentator Sayana. This yields a date of around 3000 BCE. Independent studies using modern astronomical simulation software and mathematical calculations (statistical best-fit models) indicate that the Nakshatras were closest to the path of the moon around 3000 BCE [10]. Subhash Kak has written extensively on the astronomical codes embedded within the Vedas [12].

It is clear that long before Vedanga Jyotisha, there was significant progress in time-keeping. It confirms the epistemological continuity in Indic sciences, including Astronomy and Ganita since the most ancient of times [5].

Epistemological continuity is also evident in other India's diverse traditions including art, music, dance, etc.

These prior developments are the foundation on which VJ’s calendar stands.  Let us see how VJ improves upon the prior work.

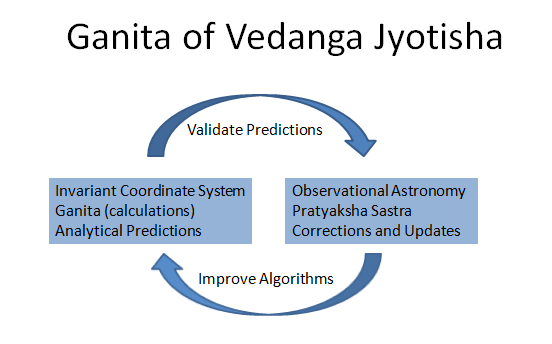
Vedanga Jyotisha’s Methods

VJ introduced an analytical time-tracking (deterministic) framework that works in tandem with astronomical observations of the real, uncertain world. Hence VJ’s Ganita calculates the timings of lunar and solar events, while also retaining and working in sync with the traditional pratyaksha sastra.  The Ganaka can make predictions, and the Nakshatra Darsa can visually confirm the degree of accuracy of these estimates, and corrections effected as needed. The diagram below illustrates how the VJ methodology can be useful in taking the science of time-keeping forward and provide increasingly accurate answers to triprasna.

Contemporary time-keeping adopts a similar approach. The atomic clock serves as an unnaturally perfect model for daily usage, but is corrected by nature. Without the latter, the model-based time would very slowly but surely drift away from reality.

The most recent leap second was added on December 31, 2016.

Nakshatra-sector Coordinate system (NCS)

Nakshatras (as stars or star groups) have been an integral part of Indic culture and some of them serve as exemplars. Dhruva (a northern pole star) and the Vashishta-Arundati (Mizar-Alcor) pair are good examples.

Prior to the VJ, the Nakshatras were used to denote visible stars or constellations (27 or 28 in number) dotting the moon’s path. Hence, it was limited by visibility.  Furthermore, these Nakshatras served as approximately fixed positions for time-keeping but were not truly invariant due to earth’s precession (‘precession of the equinoxes’). The designated pole star, for example, changes over time and cycles every 25,920 years (about a 1° shift every 71.6 years).

The Ancient Indics must have been aware of the impact of earth’s precession on the Nakshatra locations because, by the time of the VJ, the nakshatra-sectors were taken as 27 equal sections of the ecliptic (about 13.3° wide) rather than specific stars or asterisms in the background [3]. This change yields multiple benefits.

• The NCS is an invariant and uniquely Indic coordinate system that comes with a clearly specified origin (zero-point) that gives us a fixed starting coordinate. It is unaffected by the earth’s precession. The NCS resembles the modern-day ecliptic coordinate system calculation of the celestial longitude (since the moon’s path is very close to the ecliptic, tracking longitude was practically sufficient) [3].
• The NCS represents a virtualized analytical framework that allows the time-keepers to algorithmically enumerate the ecliptic sector locations of all the full and new moons in a Yuga, as well as the position of the sun. This was not possible in prior Vedic traditions since theirs was a purely physical coordinate system indentified by stars and asterisms along the moon’s path. This VJ system is free of visibility issues [3]. The VJ specifies a coordinate system using an ingenious ‘Jāvādi arrangement‘. Of course, pratyaksha continues to guide accurate time-keeping.
• This NCS helps us carry out the VJ calculations unambiguously.

Yuga

The VJ Yuga is a time cycle of 5 years of 366 days each. A five year Yuga was already present in Vedic tradition. The Yuga is an integral unit of time-keeping in the Vedanga Jyotisha and all calculations are given based on this Yuga and the NCS.  VJ assumes 12 synodic months in a synodic year plus two intercalary months (adhimasa or adhikamasa) over a Yuga to harmonize the lunar and solar calendars, giving us a total of 62 synodic months in a Yuga.  The VJ specifically includes the adhimasa as synodic months #31 and #62 of the Yuga.

A VJ Yuga is completed when the sun and moon are observed to return to the pre-specified origin region of the NCS. This is the key definition in the VJ. Here is Sri Kuppanna Sastry’s description [1]:

In other words, the Yuga begins when the Sun and the Moon are observed together in the Sravistha Nakshatra sector of the ecliptic [3].

The Parameters of a Yuga (YVJ)

Tracking the movements of spherical objects rotating and revolving around other moving spherical objects can be tricky. Here is a ‘coin rolling on a coin’ puzzle, where the inner circle serves as a fixed frame of reference. If the inner circle also rotates, then the answer is relative to the chosen frame of reference.

Earth-Sun System (days and years)

Saavana durations represent the time of the (apparent) motion of the sun relative to the earth as the frame of reference. Each saavana year in VJ lasts 366 days, giving a total of 1830 civil days in a Yuga. In reality, this frame of reference is itself slowly revolving around the sun in the same direction, and therefore saavana calculations ignore the resultant additional earth rotation (one per year). Sidereal periods are calculated with respect to a fixed reference point (e.g. distant star). The sidereal year includes this ‘missing’ rotation, giving us 367*5 = 1835 sidereal days in a Yuga. VJ’s Nakshatra Darshas would’ve observed 1835 risings of a Nakshatra (an invariant ecliptic sector) in a Yuga.

Earth-Moon System (months and fortnights)

The moon is ‘tidally locked‘ to the earth. The actual time the moon takes to go round the earth (sidereal lunar month) is the time it takes to complete a full rotation around its own axis. So one side of the moon always faces us as if it never rotates, and we never get to see the mysterious far side of the moon (photographed for the first time in 1959).

"And if the dam breaks open many years too soon 
And if there is no room upon the hill 
And if your head explodes with dark forebodings too 
I'll see you on the dark side of the moon". - Pink Floyd.

Let us calculate the number of moon rises and the number of sidereal lunar months in a Yuga. This visible side of the moon will be partially or fully observable on all sidereal days except the new moon days, of which there are 62 (one per synodic month). This gives us 1835-62 = 1768 moonrises in a Yuga, and 1830/1768 saavana days per moon rise on average.

Similar to the earth-sun system, the earth-moon system also yields an extra rotation per year depending on the frame of reference. Due to the earth’s revolution, the moon takes a couple of days extra to complete the synodic month (~29.53 days) relative to the earth. There will be 62+5 = 67 sidereal lunar months in a Yuga.

Since there are 27 sectors of the ecliptic, the moon visits 67*27 = 1809 Nakshatra sectors in a Yuga. Therefore, the moon traverses one sector in 1830/1809 = (1 and 7/603) Saavana days. The sun apparently visits 27*5 = 135 Nakshatra sectors, spending 13 and 5/9 days in a sector.

We now examine some of the larger units used in the VJ to keep time.

Larger Time Units

Saavana day: measured from sunrise to sunrise. The VJ takes the civil year to be 366 days long. Each day is divided into 124 Bhaagas (day-parts). 31 parts make a pada.

Tithi: This is a fundamental unit of the VJ equal to (1/30) of a synodic month. Hence a lunar month lasts 30 tithis, and the VJ assumes 360 tithis or 12 synodic months in a year in harmony with Vedic tradition.  Thus, a Yuga has 1860 tithis and 1830 saavana days. From this, we can calculate the VJ mean value for a tithi = 1830/1860 or 61/62 of a day.  The duration of a tithi depends on the moon’s orbit and is a variable quantity (+/- 15% the mean value), with the tithi at sunrise representing a day’s tithi [3]. Sometimes, the same tithi can mark two successive sunrises or a tithi can be lost between two sunrises. Tithi was already used in prior traditions. In the Rig Veda, atithi is a guest – one who arrives without a tithi, i.e. without prior notice [15].

A tithi can go AWOL
It can be a really close call
All ye star-crossed suitors beware
Date your Nakshatras with care!

Given the diversity of India, its calendars are also diverse. Reckoning dates for dharmic events can be tricky even in 2017. This informative subtitled video asks ‘When is Ugadi?’. Yugadi ~ start of a new yuga (new year), Hevilambi, per current Hindu lunisolar calendars.

There are also variations such as Amanta/Amavasyat versus Purnimanta calendars depending on whether the start of a month is from a new moon or full moon.

Rtu (season): Its duration is 62 tithis long, and therefore a Yuga will have 30 rtus, and 6 rtus a year. An important and unique feature of the Indian calendar is the use of six seasons including the all-important rainy season, the most celebrated and joyous of all rtus. The monsoons are governed by the annual wind patterns influenced by the Coriolis force [11]. The first rtu of the Yuga is Sishira rtu (winter).

The VJ also specifies the duration of rtu using the NCS (4 and 1/2 Nakshatra sectors per Rtu). Knowing the start date of a rtu is also important because of the Chaturmasya rite that has to be performed.

Ayana (solstice): Ayanas divide the sidereal year into two halves. There are 10 ayanas in a Yuga.

Paksha: half a synodic month, equal to 15 tithis. The bright half is the Shukla Paksha and the dark half is the Krishna Paksha. A Yuga has 62 Shukla and 62 Krishna Pakshas.

Parva: The Yuga is divided into 124 Parvas. Therefore it is equal in duration to a Paksha. The Parva Raashi (R) is the accumulated heap of Parvas since the start of a Yuga and is quantified as follows [3]: R = 2(12(y-1)+m) + p + K,

where  y = current year of the Yuga, m = elapsed months in the current year,  p is the elapsed parvas in the current month, K is an conditional correction factor (2 per 60 elapsed parvas) to adjust for intercalation.

Visuva (Equinoxes): The day when the sun apparently starts to move south or north and they occur at the mid points of each of the 10 Ayanas in a Yuga.

The interval between two successive Visuvas will be 124/10 Parvas = 12 Parvas and 6 Tithis. Hence the time elapsed in a Yuga until the N-th Equinox can be obtained by multiplying this inter-Visuva number by (N-1) and simplifying.

Bhaamsa (Amsa): To track the position of the sun and moon, every ecliptic sector is also divided into 124 equal Bhaamsas, mirroring the Parva time division of the Yuga. Hence, there are 27*124 Bhaamsas that spans the 360°. The Bhaamsa after p parvas is the remainder obtained after dividing 11p/124 [3]. The VJ rescensions state an equivalent conditional and arithmetic rule that anyone can use, similar to the previous expression for parva raashi R.

Kalaa: A day is divided into 603 parts. This number is chosen so that the time taken by the moon to traverse one of the 27 nakshatra sectors (1 and 7/603 days) = 610 Kalaas, a whole number.

VJ gives many ingenious algorithms (abhiyukti) to keep track of the number of Parva, Bhaamsa, Paksha, etc. that have passed since the start of the Yuga. The interested reader is referred to Prof. Kuppanna Sastry’s work.

Intra-day Units of Time Keeping

Researchers point to 4 different kinds of times tracked by VJ [3] apart from the cosmic time. We point these out while listing the different time-keeping units.

Akshara (2 Maatraa) ~ 0.57 seconds. Time taken to pronounce a long vowel. This  time-unit is interesting and suggests the existence of a long and well-established oral tradition.

Kaastaa (5 Aksharas) ~ 1.15 seconds.

Kalaa revisited (124 Kaastaas) ~ 2 minutes, 23 seconds. Kalaa establishes a link between the rate of speech to the average rate of lunar motion.

Naadika (10.05 Kalaas) ~ 24 minutes. Mechanically-kept time using a water clock. Passages in the Vedas [7] suggest the use of a particular water clock of the ‘overflowing type’.

Muhurta (2 Naadikas) ~ 48 minutes. Solar time based on the Sun’s apparent motion. Amazingly, the ancient muhurta measure has been preserved and passed through several generations and is used in India the exact same way, to this day.

Length of local daylight time in Muhurtas = (12 + 2N/61), where N is the number of days after the winter solstice.  Since there are 183 days in an Ayana, the maximum increase is 6 Muhurtas. Using this, the ratio of the longest to shortest day is 18/12 = 3:2. This number depends on the latitude, and therefore helps us identify the source location of VJ.

Ahoratra (30 Muhurtas) ~ ‘day and night’, or 24 hours.

Bhaaga: The local time given in 124-th parts of a day starting from sunrise. Thus we see three divisions of ‘124’ in the VJ: Parvas in a Yuga, Bhaamsas in a Nakshatra sector, and Bhaagas of a day.

Note how a speech rate is linked to lunar time, then to mechanical time, and solar time. These physical temporal cycles of varying durations are ultimately united with the cyclical cosmic time through periodic Yagna performed at the right times.

Ganita

Algorithms

The VJ approach to specifying numerical constants is pretty elegant. The high-level parameters, which are fewer in number, are enumerated. For the myriad of lower level constants that proceed down to the intra-day level, it cleverly specifies algorithms based on a linear estimate (mean motion), using rules derived from modulo arithmetic. By specifying any three independent parameters of a Yuga, all other Yuga parameters can be calculated as derived values [1].  YVJ rescension’s second verse is famous for asserting the position of Ganita as the pinnacle of sciences [1].

VJ’s methods demonstrate ancient Indic abhiyukti. They do not provide a proof of correctness, but are to be validated by pramana. When a Ganaka’s analytically predicted quantity is in conflict with observation (pratyaksha), it is the model result that is discarded, and this also forces the model to improve.

Rule of Three: Linear Estimate

The VJ uses mean motion (average rate) as a first-order approximation within its calculations using the “rule of three“.

For example: Suppose we have a known average increment for a quantity ΔQ over a time period Δt, we can calculate an average rate of change = ΔQ/Δt. What will be the accumulated value of Q after T time units? A linear estimate will simply multiply this rate by time to obtain Q = (ΔQ/Δt)*T.  The VJ states the rule of three in verse, so that it can be used repeatedly as a subroutine: calculate an average rate and multiply the increment by this rate to generate the desired output.

Modular arithmetic

The VJ works with periodic quantities that get reset to 0 after reaching a maximum value. Doing calculations with such quantities requires expertise with modular arithmetic. 3000+ years before Gauss introduced formal modular arithmetic in 1801, the Hindus were actively applying modular arithmetic for calculating a variety of elapsed and remaining time values and the positions of the full and new moons over a Yuga.

Javadi Table

The Javadi arrangement is an important contribution from a Ganita and VJ calendar perspective. It represents a virtualized (independent of stars in the background) invariant ecliptic coordinate system with a zero point taken as the new moon near the Winter Solstice, which is tied to the start of a Yuga [3]. Javadi ~ Jau Adi, i.e., arrangement of Nakshatras starting from Jau (Ashvayujau) [1]. The position of the sun and new/full moon can be located unambiguously by the Javadi name of the Nakshatra sector and Bhaamsa within that sector. The table exhibits compact data organization and a circular ordering of the NCS data so that Sravistha represents Nakshatra sector 0 (or 27).

Simple Coordinates

From the Yuga parameters and the NCS, the ‘distance’ between successive full (new) moons can be calculated as follows:

The moon passes through 1809 Nakshatra sectors in a Yuga. There are 62 full moons and 124 pakshas in a Yuga. There, the distance between two full moons is 1809/62 = 29 and 22/124 Nakshatra sectors, and a paksha length is half this value (14 and 73/124). By partitioning a sector into 124 bhaamsas, we obtain a simple  (sector, bhaamsa) coordinate system using the original Vedic ordering of Nakshatras = (N_original, B) of new and full moons, where N_original and B are whole numbers.

Order-and-Chaos

The ganita properties of the full and new moon’s bhaamsas are interesting and we did not find much discussion on this, so we make an attempt here. A brief ganita description is in the appendix at the end of the post. Let us start from a new moon at bhaamsa B(0) = 0, and add 73 bhaamsas to obtain B(1) = 73 for the first full moon, and further 73 bhaamsas to get the bhaamsa B(2) of the second new moon, and so on.  We can observe the following patterns:

1.  The full or new moon will be wandering around, visiting each and every bhaamsa number exactly once. A full or new moon will never be seen twice in the exact same location (bhaamsa) of the ecliptic within a Yuga. When it does so at bhaamsa 0 in the Sravistha sector, the Yuga is reborn (reminiscent of Kolam patterns).
2. The 62 full moons of a Yuga occur at odd numbered bhaamsas, and new moons at even bhaamsas (if we start the Yuga at bhaamsa zero). At the full moons, the Sun’s coordinates will be 13.5 Nakshatras apart, i.e 13 sectors and 62 bhaamsas away.
3. The nakshatra sector and bhaamsa are themselves linked, so if you specify just the bhaamsa, you can obtain the corresponding N_original value:

N_original = 5B mod 27 
N_original is remainder we get when we divide 5 times its bhaamsa by 27.

Of course, one can also calculate the N_original values directly as an independent check in case the input bhaamsa values are off. The VJ authors next transform the original Nakshatra sector list into the Javadi arrangement. It simplifies the required Ganita a bit (B instead of 5B).

Javadi Coordinates

The Nakshatra sector numbers can be transformed into a certain Javadi arrangement (N_original→N) using the following equation:

N = 11 N_original mod 27

Successive (original) Nakshatra sectors are 11 sectors apart in the Javadi arrangement. Conversely, successive sectors in the Javadi arrangement are 5 sectors apart in the original table. The Javadi arrangement starts from Ashvini and the final list is shown below [1]. The Sanskrit verse form of the Javadi representation is depicted at the top of this post.

Bhaamsa Generation Algorithm

This transformed N is related to B in this Javadi arrangement through a simpler modular equation compared to N_original. The (N, B) Javadi coordinates for all full and new moons of a Yuga can be iteratively generated (see appendix) and are shown in the plot below (X-axis = Javadi nakshatra sector indices, Y-axis = bhaamsa numbers). These coordinates would repeat every Yuga.

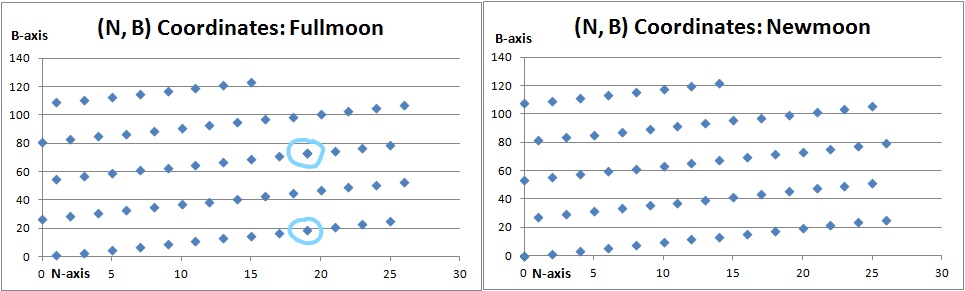
Examples

The first full moon in a Yuga is at B = 73, which gives us a remainder N = 19 when divided by 27⇒ coordinates (19, 73). Therefore, the full moon occurs in the Magha sector per the Javadi table. The next full moon will be at bhaamsa B = 73+22 = 95. Applying N = 95 mod 27 ⇒ N = 14, i.e. Uttaraphalguni (14, 95).  Multiple full moons (2 or 3) can fall in the same Nakshatra sector, but always at different bhaamsas. For example, the next and only other full moon (38-th) in the Magha sector will occur when B = (73-54) = 19. The two full moons that occur in Magha are circled in light-blue in the above picture. Note that the 3 new moons along the Y-axis at Sravistha (X = 0) are at least 54 bhaamsas (about 5.8°) apart.

Ecliptical Coordinate System

The (N, B) from Javadi are equivalent to an ecliptic longitude. These results have been compared with those generated using the modern ecliptic coordinate system, and they are quite close [3]. Tracking the bhaamsas empirically is important and this can be done mechanically using a water clock. The Javadi table is deterministic and assumes fixed synodic month duration [3], so that every Yuga starts at coordinates (0, 0). This is not so in reality, and in the next section, we can see the maximum error that is possible. Since the origin is shifted, so will the calculation for every successive full moon. While the full moons may occur in the same Nakshatra sector, the bhaamsas will be off unless the origin-shift is accounted for. The Javadi table can be used as an approximate framework/guide for the Yagna calendar and supplemented with direct observation.

We have only discussed only a few of the high-level VJ calculations. For a detailed discussion, refer to [1].

Accuracy of some VJ calculations

Mean Tithi

VJ Value = 61/62 of a saavana day.

Modern estimate of an average synodic month ~ 29.5306 days

Modern value of tithi ~ (29.5306 * 12)/360  ~ 354.367/360

Absolute Error = |354.367/360 – 61/62| < 0.05%

A Yuga has 1860 tithis, so accumulated error ~ 0.896, or less than a tithi per Yuga [2].

Mean Moonrise Rate

VJ value = 1830/1768 ~ 24 Hours 50.4864 minutes [2], i.e., the moon rises about 50.4 minutes later every day. This agrees with the modern average moonrise value really well.

Start time of a Yuga

The new moon at the start of a new Yuga may not be exactly at bhaamsa 0 of the Sravistha sector. It has been shown that up to 46 bhaamsas error can accumulate over a period of 500 years [3]. Since the moon traverses a Nakshatra sector (124 bhaamsas) in 610/603 saavana days, using the rule of three, we find that the moon traverses 46 bhaamsas in 9 hours. This is less than the minimum gap (54 bhaamsas) between successive full or new moons in the same Nakshatra sector. The maximum possible cumulative error in the start time of a Yuga after 100 Yugas is 9 hours [3].

Yuga: Self-Organizing System

In general, the VJ seems to be relatively more accurate while calculating lunar periods compared to solar periods [2]. Over the next two millennium, the Hindu lunisolar calendars were significantly upgraded. The Ancient Indics were aware of the uncertainty in the true motions of the sun, earth, and moon, and the need for corrections. The Indian comfort with uncertainty [9] is perhaps reflected in the fact that the civil calendar was deliberately set up as a simple, convenient, and approximate framework for the astronomical (Yagna) calendar. The discrepancy between the arithmetic and astronomical calendar can be fixed using an intercalary day at the end of the Yuga [1]. They also synchronized the sidereal and tropical year using appropriate corrections. Beyond these basic corrections, the lunar-solar year gap can accumulate over Yugas. It has been discovered by researchers [1, 3, 6] that the properties of the VJ Yuga yields a self-correcting system that automatically cancels out these errors.

Lunisolar correction

Five tropical years at 1350 BCE = 5*365.1734 ~ 1825.9 days

Duration of a Yuga = 62 * 29.5306 ~1830.9 days

Difference ~ −5 days per Yuga or roughly one extra day per tropical year.

If this discrepancy is allowed to accumulate over 6 Yugas (sometimes 7), the total gap will be approximately a synodic month. A Nakshatra Darsha doesn’t even need to know the Ganita behind this. He/she simply sees the sun and moon together in the Sravistha sector to signal a new Yuga. The unnecessary intercalary month 61 is automatically skipped, which resets the accumulated error.

Some corrections were made by observation of the moon phase. At the new moon the moon rises and sets with the sun. If the moon rises just after sunrise, it indicates a time near new moon. Such observations enabled the Vedics to develop the rules required for an accurate timing of the Yagnas since certain Yagna performers would incur a penalty if they erred in the timing [1]. Thus Vedic Yagna is the creative driving force that inspires this self-correcting calendar. A self-harmonizing Yuga seems natural in Prajapathi’s self-organizing universe.

Date and Source of VJ

Date

Embedded within VJ’s verses is an astronomical date-stamp about Sravistha. If α-delphini is taken as the Yogatara (principal star) of Sravistha, then between 1550 BCE and 1150 BCE, the nakshatra Sravistha and the sun would have been close at the winter solstice, i.e., the Nakshatra rises and sets heliacally at the winter solstice, and this is not possible for dates outside this period [3]. If a certain other star other than α-delphini is chosen as the Yogatara, the date gets pushed back beyond 1800 BCE [7]. Kuppanna Sastry’s ganita calculations using the earth’s precession rate, and based on the observation of the VJ author that the winter solstice was at the start of the Sravistha segment, yields dates in the range [1150, 1400] BCE. Statistical analysis of the Nakshatra system shows that a maximal proportion (80%) of the Yogataras occupy their respective Nakshatra sectors in [1300 +/-300] BCE, indicating the finalization of the NCS during this period [3]. From [5], we find mention of a date of 1255 BCE when King Suchi of Magadha, a student of Lagadha [6] set forth VJ and dated it by including an astronomical note about the summer solstice. When combined with other independent considerations such as the visibility of the Saptha Rishi (Ursa Major) from Bharatvarsha, the timing of Yagnas in conjunction with seasons, full moon, and prescribed Nakshatras, we obtain a date range [1400 +/- 300] BCE for Vedanga Jyotisha [3].

Source

Multiple works show that the Nakshatra (star) system was most likely designed around 3000 BCE [2, 3, 10]. There is clear evidence of a continuous unbroken epistemology of time-keeping from the Rigveda Samhitas to the Vedanga Jyotisha.

Independent researchers have studied the 3:2 ratio of longest to shortest day, which is only possible around a certain latitude. This includes locations in far-northern India as well as other places. The calendar with a rainy season is also special to India. By also taking into account VJ’s date, several locations get eliminated from consideration, and Kashmir appears to be a likely location of the VJ author among the feasible candidates. This has been an independent conclusion reached by multiple scholars.

The Challenge of Vedanga Jyotisha

Kuppanna Sastry has listed three fundamental requirements for a scholar who wants to study and interpret Vendanga Jyotisha in its original Sanskrit verse [1]:

• Sound scholarship in Sanskrit
• Knowledge of Western Astronomy
• Full understanding of the concepts and practices of Hindu Astronomy

Teamwork

Those who have been frustrated in this task have lacked one or more of the requirements stated above. It is not necessary for one person to have all three skillsets. We have a precedent from 3000 years ago, when Nakshatra Darshas and Ganakas combined their skills to take Indic science and technology forward. Today, traditional Vedic Pandits grounded in Sanskrit and Hindu cosmology, and STEM professionals can work as a team to overcome new challenges in many areas. The first and third requirements involve dharmic tradition, which requires shraddha and sadhana, something every team member must imbibe. The Swadeshi Indology initiative serves as an inspiring example in this regard.

Several luminaries have contributed their expertise toward explaining the time-keeping ideas of Jyotihsastra. This post summarizes the student notes compiled while learning from and exploring these truly enlightening works, which are listed in the references below.

'If you were in Darkness, what would you want more than anything else; what would it be that every instinct would call for? Light, darn you, light!' - Nightfall, Isaac Asimov.

---

References

1. KV Sarma and Kuppanna Sastry. Vedanga Jyotisa of Lagadha In its Rk and Yajus Rescensions. With the Translation and Notes of Prof. T. S. Kuppanna Sastry. Critically edited by K. V. Sarma. Indian National Science Academy. 1985.
2. Subhash Kak. Astronomy and its Role in Vedic Culture. Chapter 23 in Science and Civilization in India, Vol. 1. The Dawn of Indian Civilization, Part 1, edited by G.C. Pande. ICPR/Munshiram Manoharlal, Delhi, 2000.
3. Prabhakar Gondhalekar. The Timekeepers of the Vedas: History of the Calendar of the Vedic Period (From Rgveda to Vedanga Jyotisa). Manohar Publishers. 2013.
4. K. Ramasubramanian. Perspectives on Indian Astronomical Tradition. HH Dalai Lama Premises. Dharmasala. 2016.
5. Kosla Vepa. The Origins of Astronomy, the Calendar, and Time. Lulu.com. 2011.
6. Narahari Achar. Enigma of the Five Year Yuga of the Vedanga Jyotisa. Indian Journal of the History of Science (33). 1998.
7. Narahari Achar. A Case for Revising the Date of Vedanga Jyotisa. Indian Journal of the History of Science (35). 2000.
8. John Playfair. The Works of John Playfair (Vol. 3).. with a memoir of the author. Edinburgh, A. Constable & Co. 1822.
9. Rajiv Malhotra. Being Different: India’s Challenge to Western Universalism. Harper Collins. 2011.
10. Sudha Bhujle and MN Vahia. Possible Period of the Design of Nakshatras and Abhijit. Annals of the Bhandarkar Oriental Research Institute. 2006.
11. C. K. Raju. The Cultural Foundations of Mathematics: The Nature of Mathematical Proof and the Transmission of the Calculus from India to Europe in the 16 c. CE.  Pearson Education. 2007.
12. Subhash Kak. The Astronomical Code of the Rig Veda. Oklahoma State University, Stillwater. 2011.
13. Subhash Kak. The Wishing Tree: Presence and Promise of India. iUniverse Inc. 2008.
14. Kapila Vatsyayan. The Square and The Circle of The Indian Arts. Abhinav Publications. 1997.
15. R. N. Iyengar. A Profile of Indian Astronomy before the Siddhāntic Period. ISERVE Conference, Hyderabad, India. 2007.
16. Kuppanna Sastry. The Main Characteristics of Hindu Astronomy in the Period Corresponding to Pre-Copernican European Astronomy. Indian Journal of the History of Science (Vol 9). 1974.

Appendix & Acknowledgements

Acknowledgments: Thanks to N.r.i.pathi garu for encouraging me to write this post, and for his Baahubali-esque patience and valuable feedback.

Appendix

The bhaamsas of the full or new moon are generated using the recurrence relation:

B(k+1) = B(k)+73 mod 124.

This is an example of a linear congruential generator (LCG) that is commonly used in computer simulation models. The sequence of bhaamsas visited by the full or new moon in a Yuga are pseudo-random numbers. Since 73 and 124 are relatively prime, this LCG is guaranteed to have a full period (124) that exactly spans a Yuga. The Hull-Dobell theorem (1962) proves the result for the general case. It is also easy to see that if B(k) is even, then B(k+1) will be odd, and vice versa. We can simply generate the bhaamsas to verify this.  The following algorithm generates the chronological sequence (N(k), B(k)) of all new and full moon positions of a Yuga in Javadi coordinates:

1. Initialize: k = 0, B(0) = 0.
2. N(k) = B(k) mod 27. If B(k) is even, it is a new moon, else full moon.
3. B(k+1) = B(k) + 73 mod 124.
4. if k=123 stop. Else, k=k+1; go to step 2.