Indic Decision-Making Under Uncertainty — 1:

From Arthasastra to AI

Skip to Section 2: Decision Making under Uncertainty in Kautilya’s Arthasastra

The ability to make good decisions under uncertainty is a valuable life skill. It is also a key area in AI practice where we build systems that automate prescriptive decisions as outputs that must perform reasonably well in an uncertain environment. Practitioners are well aware of how the marketers of AI have over-promised and under-delivered in this regard. A well-received recent work that critiques AI [16] explains “why AI, so far hasn’t been on the right track, and what we might do to work toward AI that is robust and reliable, capable of functioning in a complex and ever-changing world ..”. Making good decisions with the information available today while taking into account the combined impact of random future shocks is tough.

IEEE Innovation: AI is Driving AVs, but Whose Ethics are Driving AI?This research study is in multiple parts. In this first part, we trace ideas in Kautilya’s Arthasastra relating to the fragility, robustness, and antifragility (FRA) of a system and then ask what it means to make ‘better’ decisions. Are decisions that make us less fragile, robust, or even antifragile the best we can do? FRA aside, today’s AI-embedded systems are facing increasing trust, transparency, and ethical issues.  Tacit knowledge and the wisdom of traditional knowledge systems, for example, can improve decision making. Different civilizations have had different ideas about what’s ‘better’. The latter parts of this series compare the deeper dharmic practices with the ‘western universal’ ethics and FRA ideas. We argue for a global need to embrace Indic decision making principles to uncover truly sustainable decisions in a world increasingly riddled with uncertainty.

"Overconfident reliance upon the machine may lead us into error. Rejection of the human contribution will result in systems which are inflexible and unable to respond to the unexpected". 
-Howard Rosenbrock, on the 'danger of rejecting the tacit dimension of engineering'[5].

Our primary reference is the English translation of Kautilya’s work by Dr L. N. Rangarajan [1]. Unless otherwise stated, all quotes in Section-2 are from this work with emphases in bold by this author. An alternative reference is the 1951 work of Shyamasastry [2]. Erroneous interpretations can creep into an English rendering of a Sastra full of Sanskrit non-translatables [10]. Keeping this limitation in mind and following Dharampal’s recommendations, this series explores FRA concepts as a student of India’s Ganita traditions to obtain a ‘rough and ready’ reckoning of Indic decision making.

Background

"Once I figured out that fragility was directly from nonlinearity and convexity effects, and that convexity was measurable, I got all excited. The technique— detecting acceleration of harm— applies to anything that entails decision making under uncertainty, and risk management." 

-Nassim. N. Taleb in 'Antifragile'[3].

Two articles may be useful prior reading:

i. An informal FRA discussion (2012, mildly updated 1, 2) in the dharma civilizational context.

ii. A recent article on the FRA of the Rajya-Rastra bond.

Soft Introduction to FRA

Convexity and Nonlinearity

Aerospace, Civil, and Mechanical engineers analyze the ‘elasticity’ and strength of materials used to build structures that must withstand different load configurations and stresses. Similarly, convexity and fragility are useful properties to track when designing automated decision support systems. Here’s a stock picture of a convex function f(x). ‘x’ is a varying input and f(x) is the system output in response to any input ‘x’:

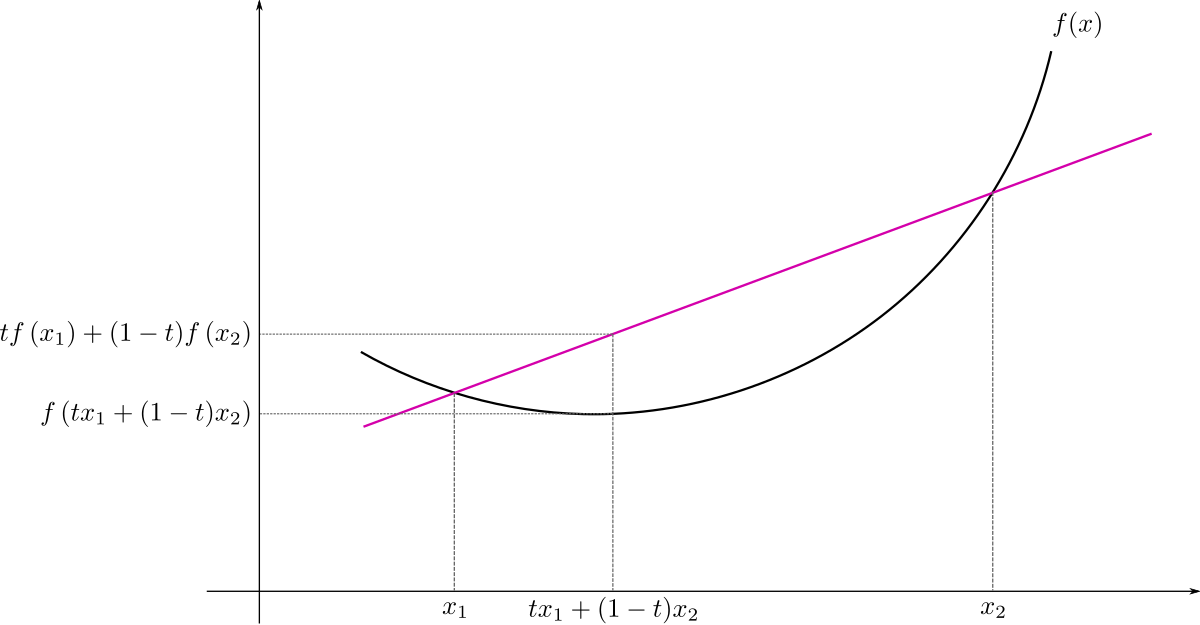
pic source: wikimedia, CC BY-SA 3.0, Link

A function f that is twice differentiable is convex on a convex set if and only if its Hessian is positive semidefinite (PSD). Practically speaking, the PSD test checks for acceleration, i.e. if the change in slope is non-negative. f(x) = x² is a simple example. A concave function is a ‘pool reflection’ of this plot. f is concave if –f is convex, e.g. f(x) = -x².

“fragility in any domain, from a porcelain cup to an organism, to a political system, to the size of a firm, or to delays in airports, resides in the nonlinear.

.. fragility equals concavity equals dislike of randomness” [3].

Following the convention in [3], a convex shape depicts increasing gains while concavity shows increasing harm. A convex function value @ average input will be less than the average of the function values @ different inputs.

“.. if you have favorable asymmetries, or positive convexity, options being a special case, then in the long run you will do reasonably well, outperforming the average in the presence of uncertainty.” [3].

A concave function’s value at average input will be more than the average of the outputs of different inputs. More uncertainty means greater harm here. If we ignore uncertainty and evaluate a system using average inputs, we may be underestimating its fragility.

“The hidden harm of fragility is that you need to be much, much better than random in your prediction and knowing where you are going, just to offset the negative effect.” [3].

Queuing Example

We’re standing in line to process paperwork in a government office. Customers arrive at an average rate (A) of 10 per hour and the clerk processes an average (S) of 12 requests per hour. Our wait time could be zero if we ignored uncertainty: every request is processed in 5 minutes and every customer arrives 6 minutes apart. If there’s significant uncertainty in the inter-arrival and service times (following “M/M/1“), the expected time (T) in the office is 1/(S-A) = 1/(12-10) = half-an-hour. If we fixed S and varied the input A, the output function -T is concave wrt A.

After a heavy lunch, if the clerk processes just one less paper per hour, the new T = 1/(11-10) = one hour. i.e., the loss doubles. If the arrival rate increases by just one person per 2 hours, T doubles again = 1/(11-10.5) = 2 hours. This is an example of nonlinear harm caused by congestion and becomes a headache for the Sarkari officer. On the other hand, the chaiwallah’s income from these customers is convex. He only benefits from this uncertainty. In practice, we don’t have to depend on some “M/M/1” model and can directly observe and track the changes in wait time as ‘x’ varies.

Fragility – Robustness – Antifragility

For precise definitions of FRA, refer to Prof. Taleb’s technical paper. Here, we’ll use an informal example derived from his book: Suppose we ship an item in a box that is subjected to a series of external random shocks during transit. Upon delivery, we open the box and examine the contents.

Fragile item: broken. It reacted badly (concave) to shocks.

Robust item: remains the same. It was indifferent to shocks.

Antifragile item: got better. It thrived on (convex to) the shocks.

Now imagine a country of 1.4 Billion people in a box being subject to random shocks from a mysterious infectious virus as well as a variety of other internal and external threats. What would be the combined impact? The government’s decisions would have to protect against the consequences of the uncertainty regarding the nature and impact of a mystery virus.

Prof. Taleb’s technical paper presents a fragility detection heuristic, including a version based on finite differences rather than abstract infinitesimals. This is in the spirit of Ganita that deals directly with reality. For e.g., the Aryabhatiya’s finite difference formulas for fine-grained Sine values are real-world representations of ordinary differential equations [6]. The heuristic examines the changes in the response to multiple changes (e.g. a 10% increase and decrease) in the critical input levels.

For this discussion, shocks are classified into two types:

1. High-probability low-cost (linear, HPLC): repeated shocks (e.g. coastal waves during seasonal storms) that show up in the historical data.
2. Low-probability high-cost (concave, LPHC): few or one extreme hazard (e.g. big tsunami) that may not even show up in the past data available to the decision maker.

"Nobody will buy a home robot that carries their grandfather safely into bed four times out of five" -[16].

Today’s AI is fragile. A “data driven” mechanistic AI approach would only accept what is seen and ‘overfit’ decisions to available data (HPLC) and ignore LPHC considerations. Good decisions prioritize protection against LPHC shocks. However, it is difficult to estimate the tiny probabilities associated with individual LPHC events and even small model errors can produce big distortions [3]. In a karmic world with a garden variety of LPHC events, something’s bound to give. A simpler way is to identify and rank the severity of threats should they materialize and protect against their impact, or even gain from certain shocks (antifragile) by acquiring and taking advantage of options. This is Kautilya’s approach.

Additional Terms used by Prof. Taleb

i. Options– When you aren’t sure about what’s going to happen, it is good to have a plan B and C (“no plan survives contact with the enemy“).

“The option is an agent of antifragility.

If you “have optionality,” you don’t have much need for what is commonly called intelligence, knowledge, insight, skills, and these complicated things that take place in our brain cells. For you don’t have to be right that often. All you need is the wisdom to not do unintelligent things“. -[3]

A lesson in democracy from the 2016 and 2020 US Presidential elections is that the absence of indigenous social media platform options will sharply increase India’s information fragility during uncertain time periods such as the general elections in 2024. Commercial interests cannot supersede national interest, which leads us to the next point.

ii. Path dependence: what’s broken cannot be unbroken.

“A package doesn’t break under adverse conditions, then manage to fix itself when proper conditions are restored. Fragility has a ratchetlike property, the irreversibility of damage. What matters is the route taken, the order of events, not just the destination — what scientists call a path-dependent property.” – [3].

iii. Barbelled portfolio: combination of two very different investment alternatives that understands and works with path-dependence.

“Barbell Strategy: A dual strategy, a combination of two extremes, one safe and one speculative, deemed more robust than a “monomodal” strategy; often a necessary condition for antifragility.”

“the barbell [is] a domestication, not the elimination, of uncertainty.” – [3]

The remainder of this post summarizes Kautilyan decision making under uncertainty. The study is not exhaustive but shows that the key principles underlying the modern western approach to decision making under uncertainty were already well-understood in Indic decision making, codified in an Artha Sastra, and practically applied by the time of Kautilya.

FRA in Kautilya’s Arthasastra

(Unless otherwise stated, all quotes in Section-2 are from Dr. LN Rangarajan’s work [1] with emphases in bold by this author)

Many Arthasastras

For brevity, the reader is referred to ICP’s articles and critique [7, 8] of Kautilya’s work on statecraft. There is an ongoing debate on the time period of Kautilya, also known as Chanakya and Vishnu Gupta. Pandit Chelam dates his lifetime to ~1500 BCE and recognizes him as a contemporary of Chandragupta Maurya. They predate the Macedonian invaders who were defeated by a different Gupta around ~300 BCE. Colonial western historians identify the latter as Chandragupta Maurya and cite this more recent date. A recent study by Indian scholars documents multiple issues with the colonial approach to Indian chronology [11].

We do not want to overstate Kautilya’s influence on Indic decision making. His work is not the first Arthasastra [8, 9]. Prior discussions with overlapping content can be found among the works of Brihaspati, Narada, the discourse in the Shanti Parva and the Vidura Neeti in the Mahabharata [7], and can be traced back to the Vedas [9]. It would not be surprising if some of the ‘Kautilyan decision making’ ideas summarized below were developed earlier.

The ancient Itihasa Mahakavyas (Ramayana and Mahabharata) have served as a guiding light to critical decision making in India and have withstood the ultimate test of fragility and uncertainty there is – of time. The scope of Kautilya’s treatise is far narrower than these sacred texts and this limitation makes it a convenient entry point for our study:

“Arthashastra is concerned with the security and foreign policy needs of a small state, in an environment with numerous other small states.

Kautilya uses four devices to derive practical advice for specific situations from his essentially theoretical concepts. These are: relative power, deviations from the ideal, classification by type of motivation, and the influence of the intangible and the unpredictable.”

Calamities (Vyasanas)

Kautilya first assesses how a small state will perform when subjected to one or more calamities. A vyasana is any event that causes any component of the state to be absent or operate sub-optimally. Vyasanas include acts of God that are quite unpredictable. Kautilya’s categorization and assessment of vyasanas is comprehensive and clinical. For example, he studies 34 different calamities that can potentially degrade just the state’s military capacity. Rather than being reactive, he recommends proactive measures today to neutralize future vyasanas.

“In the interests of the prosperity of the country, a king should be diligent in foreseeing the possibility of calamities, try to avert them before they arise, overcome those which happen, remove all obstructions to economic activity and prevent loss of revenue to the state.” {8.4.50, 8.5.21}

… Kautilya uses the word ‘calamity’ (vyasana) in the precise sense of any event which weakens any constituent element of a state, thereby preventing it from being used to its full potential in the conduct of foreign policy or war.

… Calamities can be due to Acts of God or men and may arise from misfortune or bad policies.”

Kautilya does not rank the vyasanas on the likelihood (probability) of occurrence. He enumerates the various types of calamities and records its potential severity (cost) on the various components of the state. For example, fire, famine, flood, and pandemics are four different calamities that have different dimensions of damage including extent, magnitude, etc. He creates a rank order list of components that are most to least critical to the state. This list helps identify calamities that are more critical to the stability of the state. This is different from ranking threats on just magnitude.

Path Dependence

Kautilya prioritizes survival over profits.

“no one would want to lose his own life even for a large sum of money.

Kautilya frequently warns that both present (short-term) advantages and future (long-term) advantages have to be taken into account. For example, {7.8.5-10} show when to forego short-term advantages, or even any advantage, when concluding treaties.

.. Kautilya suggests that one should take into account the overall benefit which includes the immediate gain as well as the potential future gain. Sometimes, it may even be advisable to forgo any apparent benefits.’”

Kautilya’s ranking of state elements is based on the increase in the fragility of the system due to that element’s partial or complete loss due to a vyasana. A numbered list has been presented for clarity.

“Some teachers have said that: ‘Of the calamities befalling the

1. king,
2. the ministers,
3. the populated territory,
4. the fort,
5. the treasury,
6. the army and
7. the ally,

that which affects the one mentioned earlier in the order is more serious than that affecting one later.’ {8.1.5} [Other teachers, however, hold that a calamity of a constituent lower in the order could sometimes be more serious than that of the one immediately preceding.]

… what Kautilya calls the ‘interest of the king’ would nowadays be termed ‘national interest’.

If we were to plot the increase in a small state’s fragility (i.e., negative gain) due to the absence of each component, we’d end up with something like the concave shape below (*see footnote).

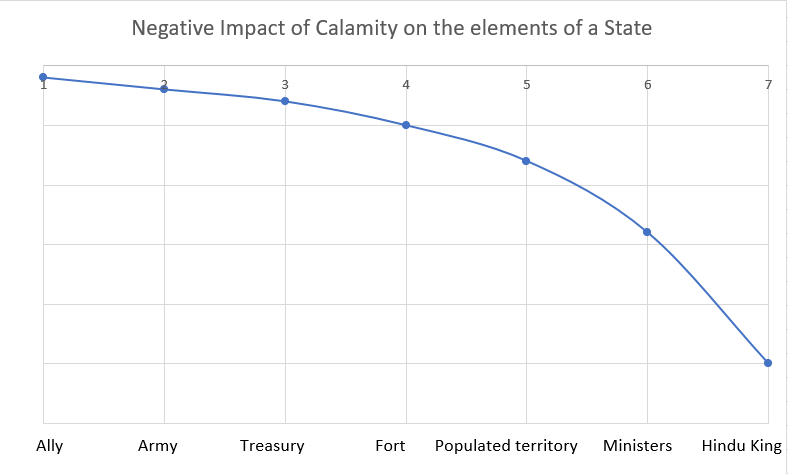
Kautilya uses this rank list to prescribe a policy specifying the sequence and level of escalation to be followed:

The conqueror shall save from misfortune, one by one, the constituents of his state, in order of their importance;

[note: conqueror ~ king]

The least important [constituents or parts of constituents] shall be saved by peace, inactivity or a dual policy and the most important by other means [seeking help, preparing for or actually waging war.] {9.7.46-50}“.

Options

Kautilya’s understanding of the value of options and path dependence is masterly. This is also evident in this ‘fort > treasury’ argument:

“[A fort has many uses.] The treasury is kept safe there and the army is well protected in it. It is from the fort that secret war is waged, one’s own people controlled, allies received and enemy troops and jungle tribes kept at bay. In the absence of a fort, the treasury will fall into the hands of enemies. It is well-known that those with forts are not destroyed.”

Kautilya examines a scenario where a royal family member or high ranking official or even the king may need to be handed over to a rival king as a hostage to ensure adherence to an unfavorable treaty that was signed. When the king has flexibility in the choice of hostage, Kautilya identifies the best option based not just on minimizing the downside but also maximizing the potential upside. His first choice is a treacherous minister (second most fragile state element). Having options makes the king antifragile to keeping or breaking the treaty.

“The list starts with a treacherous minister who is, in fact, intended to be a victim; since the hostage giver does not care what happens to the hostage, he can break the treaty when it suits him! The last person who shall be offered as a hostage is the treaty-maker himself.”

Fragility

When comparing two elements affected by a calamity, Kautilya compares a) their damage (incremental loss) so far, and b) the rate of change of damage:

“When two elements are affected equally, they should be judged according to whether the damage is increasing or decreasing, so long as neither of them affects any other element. [When two elements are equally and simultaneously affected, that which is likely to suffer increasing damage should be considered more serious. {8.1.62}”

Kautilya compares acceleration to determine which situation is more serious and goes deeper into nonlinearity and higher order effects:

“However, if the calamity to one element is likely to affect other elements, then that should be considered more serious.]”

Some teachers say that fire is more serious than floods because destruction by fire is irremediable, consuming all; one can escape from floods and its damage can be alleviated. Kautilya, however, considers floods to be more dangerous because it destroys hundreds of villages while fire destroys [only] one village, or a part of it.

[The reasoning is: floods and famine, which affect agricultural production, the livelihood of people and state revenue are more serious than fire and disease, the effects of which tend to be more local.

Gambling with one’s property and betting on animal races leads to a win for one and a loss to the other. The consequence is that factions are formed and strife ensues.”

Another example is the critical decision between war and peace. Kautilya recognizes that war comes with hidden fragilities and cascading (increasingly nonlinear) consequences that make it less preferable to peace if both appear to be equally effective on the surface.

“When the degree of progress is the same in pursuing peace and waging war, peace is to be preferred. For, in war, there are many disadvantages, such as loss of troops, expenditure and absence from home.

The Kautilyan ranking of severity is based on fragility (concavity). This principle stated more than 2200-3500 years ago is effectively the same as that in the modern PSD check and fragility detection heuristic. Like other scholars of dharma, Kautilya’s understanding of the implications of an interconnected world is clear. The consequences of interconnectedness are discussed in depth by Prof. Taleb [3] as well as in this Arthasastra.

We’ll close with an interesting example where Kautilya goes beyond local fragility or convexity. He compares the longer-term nonlinear trajectories of the progress or decline of initiatives in his own state versus the enemy state before deciding to intervene. If he expects positive convexity (∪-shaped recovery) where it may get worse before it gets better for his own state, or a concave decline (∩-shaped) for the rival state, it may be optimal to do nothing even though the enemy is leading and gaining today.

“A king suffers a decline when his own initiatives are ruined or when the enemy’s undertakings prosper. [However,] a king may ignore an enemy’s progress if he believes that his own decline will be of shorter duration or lesser extent before progress is resumed and that the converse will apply to his enemy. {7.1.24-26}“.

Robustness

Supply Chain Fragility and the Kautilyan Safety Stock Equation

The Arthasastra recommends a conservative safety stock level (reserve) that is equal to the demand (i.e. base stock = twice the demand (D) expected until the next replenishment). This prescription reduces the possibility of stocking out due to a disruption in the supply chain by a vyasana. Local availability is assured whereas the on-time arrival of imports from outside the fort or state is concave to uncertainty.

The Chief Superintendent of Warehouses has to keep half the quantity of the commodities in store as reserve stock for use in times of calamities and use only half for current needs. To be even more prudent, he is asked to replace regularly old stock with new {2.15.22,23}… ”

Kautilyan Safety Stock (SS = D) vs Modern Inventory Planning Systems

First note that Kautilya is simultaneously recommending demand-side management, i.e., to curtail consumption as required and be self-organized (a key Vedic principle). He thus eliminates demand uncertainty from the equation and only has to protect against uncertainty in ‘lead time’ (LT = time until new supplies arrive). The following mathematical formula [15] is used today to calculate safety stock (SS) under uncertain lead times:

SS = LT deviation X desired service level X consumption rate.

Typical chosen values for the service level based on the normal random distribution is 1.3 (> 90% availability) to ~1.7 (> 95% availability). We can rewrite the variation as follows:

Coefficient of Variation (CoV) = deviation / mean,  so that

LT deviation = Avg Lead Time X CoV

The LT CoV is between 5% to 50% depending on the supply chain reliability, yielding a conservative SS = 1.7 * 0.5 * (Avg Lead time * consumption rate) = 0.85 * Demand.

Kautilya uses a more conservative SS value = 1.0 * Demand.

The Kautilyan safety stock (SS = D) allows a self-organized state to survive an entire restocking cycle without any external dependency.

By additionally curtailing consumption and always keeping fresh stock, the state can hold out even longer than an adversary expects.

In July 2020 when Covid-19 had spread all over North America, a leading supply chain management expert recommended exactly this Kautilyan safety stock to minimize supply fragility [13] due to the pandemic:

“… in a world of volatility, logisticians can no longer afford to assume stability.

“If a disaster is anticipated, logisticians should build safety stock equal to at least demand during lead time for the important items. So, if expected lead time is 50 days and daily demand is 100 units, hold 5,000 units in stock. These items could be warehoused in a centralized location, as long as fast transport is available when needed.” – Prof. Paul D. Larson [14].

The Kautilyan Safety Stock formula is implicit in the savings approach of Bill Gates when Microsoft was a small company in the midst of technological disruptions and uncertainty: “From the day he started Microsoft he insisted on always having enough cash in the bank to keep the company alive for 12 months with no revenue coming in. In 1995 he was asked by Charlie Rose why he kept so much cash on hand. Things change so fast in technology that next year’s business wasn’t guaranteed ..” – [17].

Antifragility

Profit and Wealth

Examine the directive for foreign trade:

A crucial injunction regarding trade with foreign countries given to the Chief Controller of State Trading is: ‘generate profits; avoid losses’. {2.16.25} The regulations for buffer stocks and futures emphasize profitability {2.16.2,3; 4.2.36}.

A focus on generating profits alone would inject fragility. By avoiding losses, one seeks robustness. By combining them, one can design an antifragile trade policy that keeps the upside while removing the downside. There is also a clear distinction made between the different types of returns from ventures.

“Even a large profit shall be foregone if it is likely to cause harm to the public. {2.16.6}.

… Artha ’ is used in this chapter in a very special sense, always combined with an adjective— ‘ aapadartha ’, a risky return or acquisition and ‘ anartha ’, a debacle in the sense of a wrong acquisition.”

When deciding between two investment options (military campaigns) that appear to generate equal gain on the surface, Kautilya employs a multi-criteria nonlinear test to determine the better option. He compares the acceleration, longer term increase in fragility, the distribution of the gain, etc.:

“When the gains [from two campaigns] are equal, the king shall compare the following qualities and choose that one which has more good points: – place and time; – the power and the means [required to acquire it], – the pleasure or displeasure [caused by it]; – the speed or slowness [of getting it]; – the proximity or distance; – the immediate and future consequences; – its high value or constant worth; 6 and – its abundance or variety. {9.4.24}“

In other words, the best wealth gain is that which promotes Dharma and Purusharthas and is fractal. An explicit role for dharma, a key Sanskrit non-translatable, in the ethics of FRA is unique to Indic decision making:

“Wealth is like a tree; its roots are dharma and the fruit is pleasure. Achieving that kind of wealth which further promotes dharma, produces more wealth and gives more pleasure is the achievement of all gains (sarvarthasiddhi).”

Portfolio Optimization and Asset Management

“ The king was advised to maintain a diversified economy ..”

Kautilya’s recommendation of a diversified portfolio or ‘risk pooling’ is popular to this day. He aims for a specific mix that consists of only a few high value/specialized assets having potentially uncertain returns but is dominated by a large number and variety of low value assets that are likely to generate steady if unspectacular returns. What is the benefit? This bimodal portfolio would not incur any significant loss but occasionally yields excellent returns, i.e., antifragile and resembling the ‘barbell‘ approach of Prof. Taleb. This principle is expressed multiple times in the Arthasastra.

… It was better to have a large number of trade routes even if they were not all built to high standards.

… Kautilya believed that it was better to have a large production of low value minerals than a small production of high value ones {7.12.13,16}.

… Kautilya believed that a large number of comparatively dull elephants was preferable to a few brave ones {7.12.8,11} and that elephant forests were more important than other kinds because ‘one depends on elephants for the destruction of the enemy’s forces’ {7.11.13-16}.”

Beyond FRA

The overarching principles rooted in the Vedas that govern decision making are Satya → Rta → Dharma as explained here. FRA only comes afterward and this is a fundamental difference between the Western Universal (WU) decision making that drives today’s AI and the Indic way. Even some of Kautilya’s contextual recommendations have been criticized by Bharatiyas [7, 8]. While Kautilya did not ignore dharma or the Purusharthas, it has been debated whether his recommendations accorded dharma the highest priority.

“… These were either required because the interests of the state demanded it or because the persons against whom these were directed were enemies of the state {5.2.69}. These methods were not to be used against those who were neither evil nor treacherous.

Just as Kautilya’s important qualifications to his advocacy of unethical methods is often ignored, so is the voluminous evidence in the Arthashastra of his emphasis on welfare, not only of human beings but also of animals. Welfare in the Arthashastra is not just an abstract concept...”

Kautilyan methods certainly benefit a small state. However, if many states employed these methods to become antifragile at the expense of an increase in Bharata’s fragility and a decline in dharma, that is clearly not a sustainable outcome. The ancient wisdom of the Vidura Niti [12] reflects the dharma of FRA and path dependence:

atma > earth > kingdom > village > family > individual.

It is not clear that FRA based AI/human decision making subject to WU ethical caveats are sustainable. Before we study how our dharmic practices and sacred texts can resolve this issue, it is worth reviewing the works of key western thinker-doers who helped shape modern FRA ideas.

Author’s Footnote

*the path dependence list only tells us the relative order of importance. We can however recover a concave shape of this fragility graph by examining its reflection, i.e. the nonlinear increase in escalation recommended by Kautilya from Left to Right.

References and Further Reading

1. L. N. Rangarajan. Kautilya: The Arthashastra (Translation). Penguin Books. 1987.
2. R. Shyamasastry. Kautilya’s Arthasastra. Mysore Press. 1951.
3. Nassim N. Taleb. Antifragile: How to Live in a World We Don’t Understand. Allen Lane. 2012.
4. Nassim. N. Taleb and Raphael Douady. Mathematical Definition, Mapping, and Detection of (Anti) Fragility. https://arxiv.org/abs/1208.1189. 2012.
5. Artificial Intelligence, Culture and Language: On Education and Work. Bo Goranzon and Magnus Florin (Editors). Chapter 12: Engineering as an Art. Springer Verlag. 1990.
6. C. K. Raju. The Cultural Foundations of Mathematics. The Nature of Mathematical Proof and the Transmission of the Calculus from India to Europe in the 16th C. CE. Pearson Longman. 2007.
7. N. R. I. Pathi. On Koota Niti. Indicportal.org. 2019.
8. N. R. I. Pathi. On Rajadharma. Indicportal.org. 2018.
9. Handbook of Hindu Economics and Business. H. D. Vinod (Editor). CreateSpace. 2013.
10. Rajiv Malhotra and Satyanarayana Dasa Babaji. Sanskrit Non-Translatables : The Importance of Sanskritizing English. Amaryllis. 2020.
11. Manogna Sastry and Megh Kalyanasundaram. The A of ABC of Indian chronology: Dimensions of the Aryan problem revisited in 2017. Land of Dharma – Proceedings from Swadeshi Indology Conference Series, 2019.
12. Vidura Niti. Sanskrit Text With English Translation by KM Ganguli.
13. Emily Atkins. Seven ways the pandemic will change supply chain management. 2020.
14. Paul D. Larson. Is Just-in-Time out of time? JIT is built on the assumption of stability, but in a world of volatility, logisticians can no longer afford to assume stability. 2020.
15. Peter L. King. Crack The Code. Understanding safety stock and mastering its equation. web.mit.edu. APICS Magazine. 2011.
16.  Gary Marcus and Ernest Davis. Rebooting AI: Building Artificial Intelligence We Can Trust. Pantheon. 2019.
17. Morgan Housel. Save Like A Pessimist, Invest Like An Optimist. Collaborativefund.com. 2020.